解答欄
解説
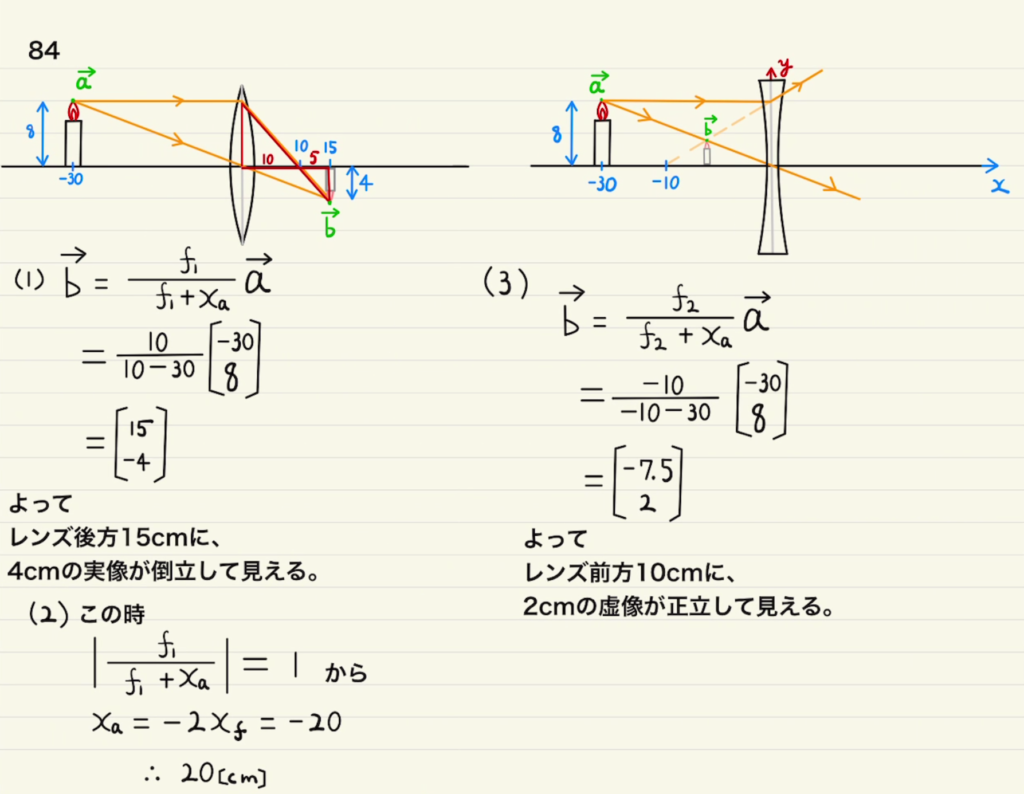
(1)(3)はレンズの式に当てはめるだけです。
ここで導いた拡張したレンズの式
$$ \vec{b} = \frac{f}{f+x_a} \vec{a} $$
を使うと、像の大きさや位置もすぐに求まります。
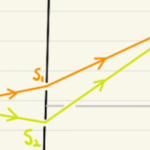
(1)では凸レンズなので$f$は正であり、計算すると $x$成分が正の実像、 $y$成分が負の倒立となります。
(3)では凹レンズなので$f$は負であり、計算すると $x$成分が負の虚像、 $y$成分が正の正立となります。
図も描くことで位置が間違っていないことも確認できます。
(2)は倍率 $|\frac{f}{f+x_a}|$が$1$であることから位置を逆算するもので、絶対値の中身が正だとすると $x_a=0$でレンズと重なるのでありえず、 $\frac{f}{f+x_a}=-1$から計算できます。 (ろうそくの位置の$x$座標$x_a<0$を満たしていますね。)
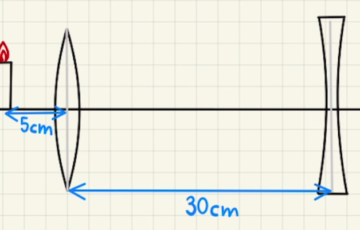
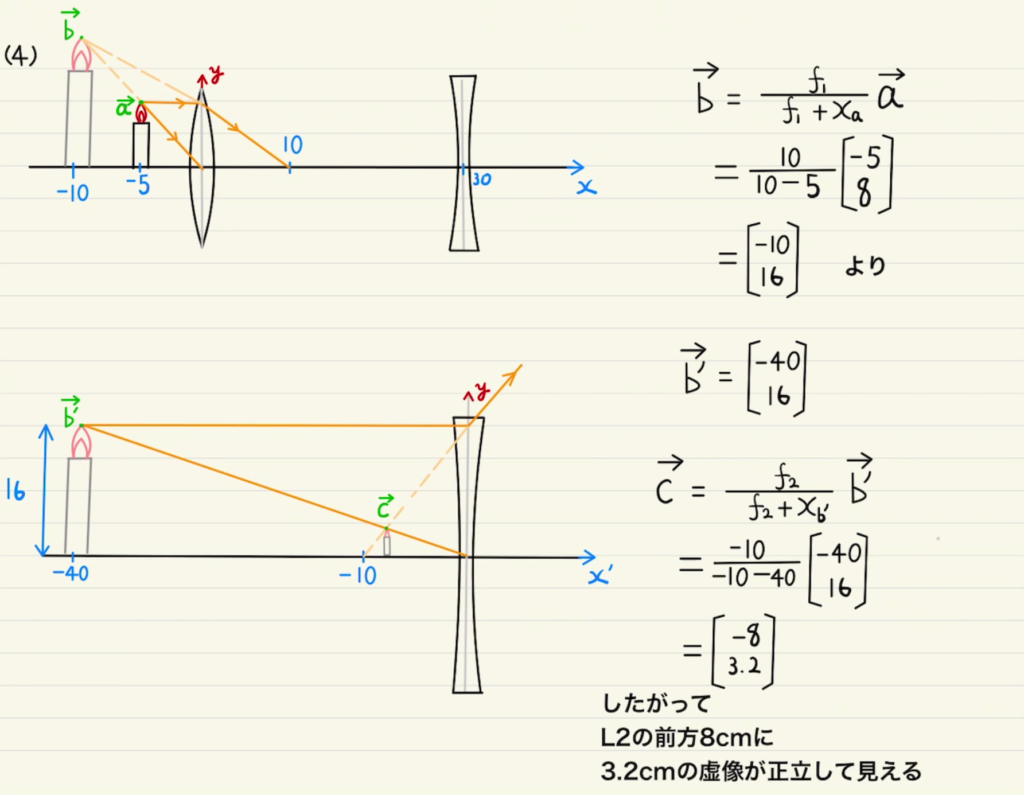
(4)は二つのレンズの合成レンズの問題です。
一般的には$L_1$の像をさらに$L_2$により二つ目の像を映すというやり方で計算できます。
$L_1$の像を計算するときの原点は$L_1$の中心で、 $L_2$の像を計算するときの原点は$L_2$の中心になることに注意しましょう。
$L_1$の像の位置ベクトル$ \vec{b}$は$L_1$からの位置を使っているため、$ \vec{b}$は$L_2$からの位置ベクトル $ \vec{b’}$に書き換える必要があります。
$ \vec{b’}$ から二つのレンズの像 $ \vec{c}$を計算できます。 $ \vec{c}$ も $L_2$からの位置になるので注意しましょう。
合成レンズに書いたように
$$ \vec{b_2} = \frac{f}{f+x_{a_1}} \vec{a_1} $$
を使うこともできます。