解答欄
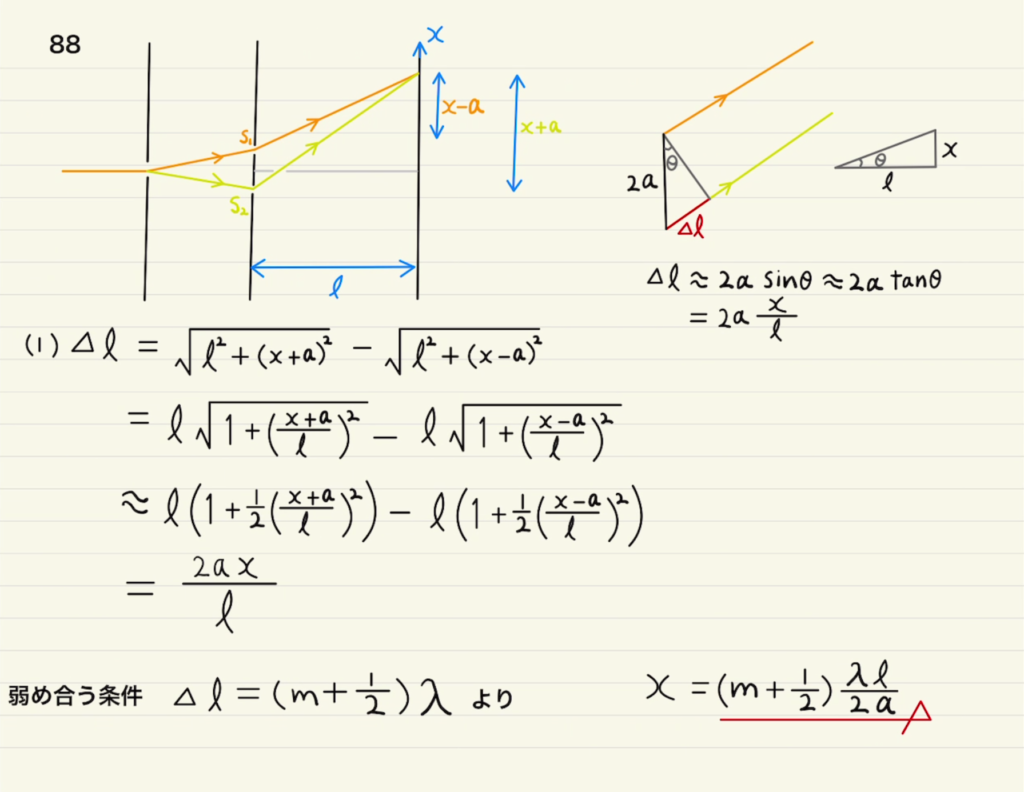
解説
いわゆるヤングの実験というもので、二つのスリット(隙間)から入った光の経路が異なることで光が強め合ったり弱めあったりするものです。これにより光は波の性質を持つことが証明されました。
当時は太陽光を使用していたため様々な位相の光が混在しており、スリット1で位相が同じ光だけを通す必要がありました。レーザー等でやる場合には必要ありません。
移動経路はルート引くルートの形で複雑なので、近似して計算します。
(1)近似方法は一般的に二つの説明のしかたがあります。
一つ目は一次近似の計算による方法です。
$|δ|<<1$のときに$(1+δ)^n≈1+nδ$として扱う一次近似を使います。
今回は$√$なので $(1+δ)^\frac{1}{2}≈1+\frac{1}{2}δ$ となりますね。 ここでは、$δ= (\frac{x+a}{l})^2$ となります。
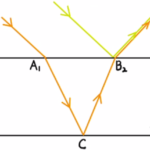
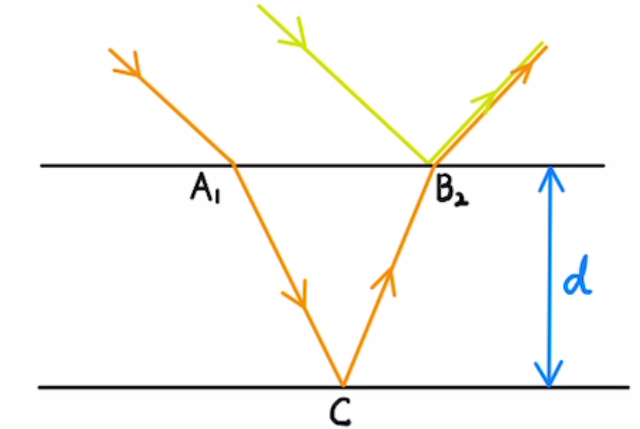
二つ目は図のθの角度は非常に小さい→光がほぼ平行と扱うものです。
このとき、垂直に下した部分までが経路差となります。
また、$\sin{θ}≈θ≈\tan{θ}$の近似も必要となります。
近似をすると経路差は$x$に比例する形になるので、干渉縞は等間隔になると言えます。
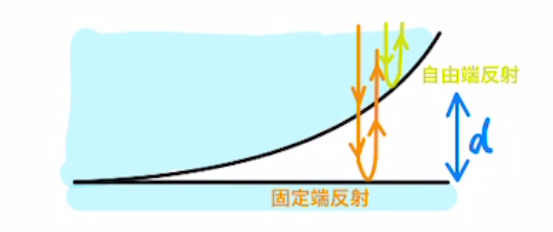
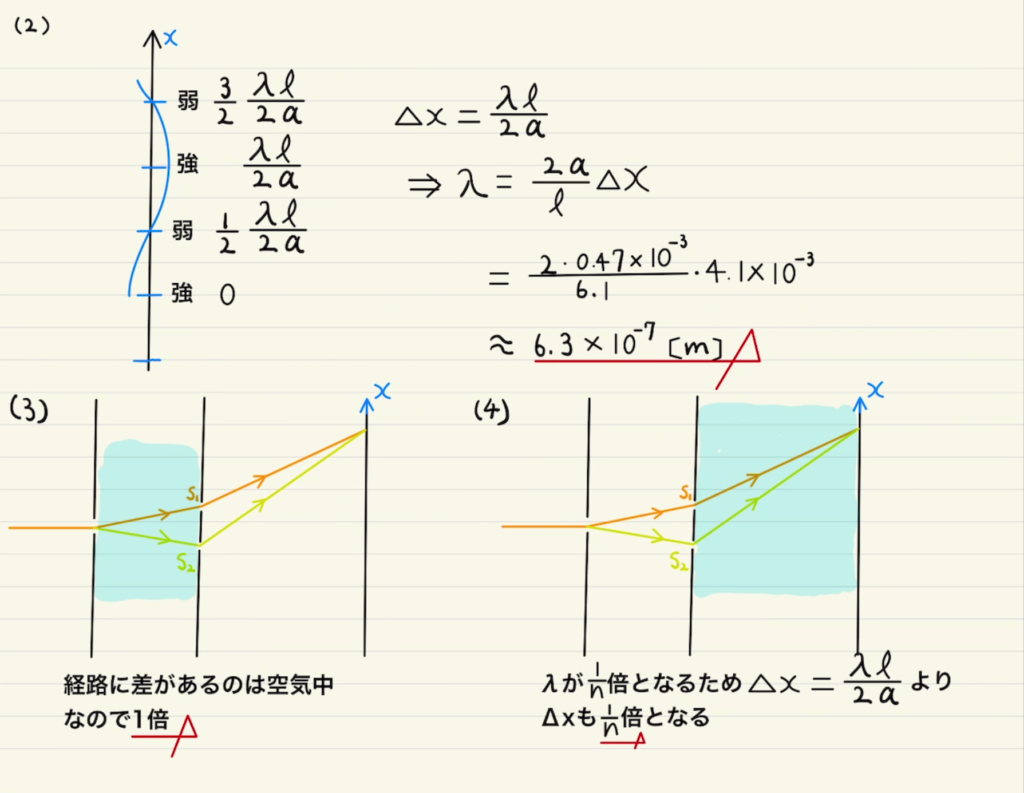
(2)経路差が$0,λ,2λ,3λ…$のときは強め合うことで明るくなり、 経路差が$\frac{1}{2}λ, \frac{3}{2}λ, \frac{5}{2}λ …$ となるときは光は弱めあい、暗くなります。
そこから逆算して、光の波長$λ$を計算することができした。
(3)(4)屈折率$n$の媒質の中では光の速さ$c$は$\frac{1}{n}$となり、振動数$f$が一定なことから光の波長$λ=\frac{c}{f}$も $\frac{1}{n}$となります。
位相差で考えることもできます。
波の式$ y(t , x) = A\sin{2π(\frac{ t }{T} – \frac{ x}{λ})}$の位相は$ 2π(\frac{ t }{T} – \frac{ x}{λ})$となります。 同じ時刻でスリット1に入ってきた光はほぼ同じ時刻でぶつかるため、位相差は$ -2π\frac{Δl}{λ}$となるため、 λが $\frac{1}{n}$となれば経路が変わらない場合の位相差は $n$倍となります。
屈折率$n$の媒質中での光が距離$l$だけ進むときの位相変化は、真空中では距離$nl$だけ進むのと同じであるため、 $nl$を光学的距離と言います。
位相も真空中の$nl$進んだのと同じ分だけずれるので、
$nΔl = (m+\frac{1}{2})λ$と表すこともできます。