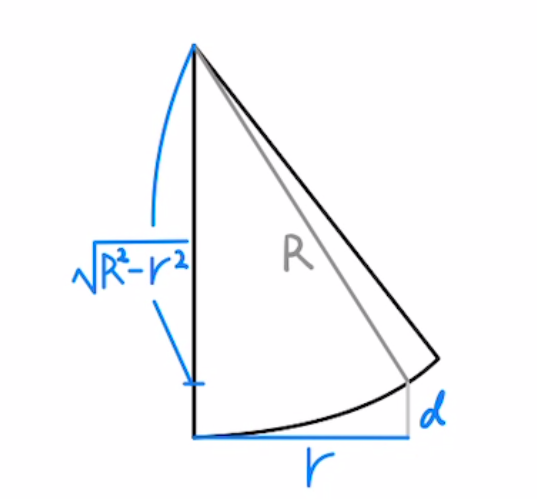
(1)空気の厚みは
$d=R-\sqrt{R^2-r^2}$
$=R-R\sqrt{1-(\frac{r}{R})^2}$
ここで$|δ|<<1$のときの一次近似 $(1-δ)^n ≈ 1-nδ$であることを使うと、
$d= R-R\sqrt{1-(\frac{r}{R})^2} ≈R-R(1-\frac{1}{2}(\frac{r}{R})^2)$
$=\frac{r^2}{2R}$__答
となります。
この時経路差は$Δl=2d= \frac{r^2}{R} $となり、$r^2$になることがうかがえます。
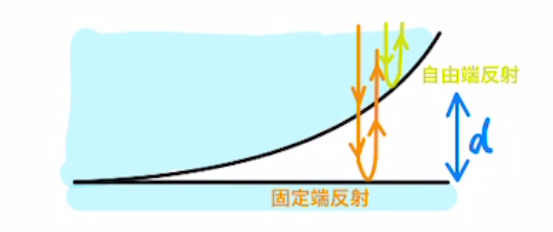
(2)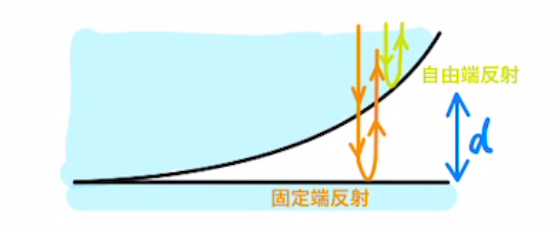
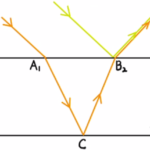
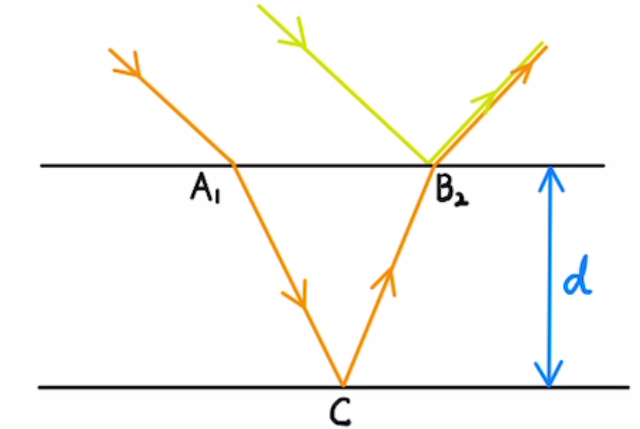
図の黄色線の光は、屈折率が大→小で反射するため、自由端反射で位相はズレません。
オレンジ色線の光は、屈折率が小→大で反射するため、固定端反射で位相がπズレます。(波長では$\frac{λ}{2}$分)
このことから、光が弱めあう条件は
$Δl+\frac{λ}{2} = (m+\frac{1}{2})λ$
となるため、
$ \frac{r^2}{R} +\frac{λ}{2} = (m+\frac{1}{2})λ ⇒ r=\sqrt{mRλ}$
同様に、光が強め合う条件は
$r=\sqrt{(m – \frac{1}{2} )Rλ}$
となります。
今回ですと、$r=0$付近では$m=0$の弱めあう条件に合うため、中心部付近では暗く見えます。 __答
また、中央から暗線までの距離は$\sqrt{r}$に比例するため、暗線の間隔は次第に狭くなっていきます。

また、可視光では赤の波長$λ$が長く、青の波長が短い。
そのため、 赤のほうが$r=\sqrt{(m – \frac{1}{2} )Rλ}$ が大きくなるため、外側は赤色となります。
(3) 先ほどの強め合う式$r=\sqrt{(m – \frac{1}{2} )Rλ}$ に$m=1,2,3$を代入していくと
1番目:$ r_1=\sqrt{\frac{1}{2} Rλ} $
2番目:$ r_2=\sqrt{ \frac{3}{2} Rλ} $
3番目:$ r_3=\sqrt{ \frac{5}{2} Rλ} $
となる。
設問分から、 $ r_3 = 3.0[mm] = 3.0×10^{-3}[m]$なので
$R=\frac{r_3^2}{\frac{5}{2}λ}= \frac{ (3.0×10^{-3})^2 }{\frac{5}{2}×540×10^{-9}} ≈ 6.7[m]$ __答
となり、(1)で前提としていたr<<Rはたしかに成り立っていますね。
(4)
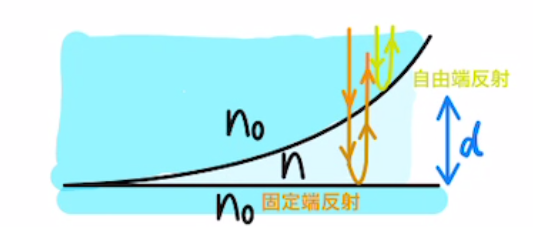
中に入れる液体の屈折率$n$がガラスの屈折率$n_0$より大きいか小さいかで固定端反射する場所が変わりそうです。
(ⅰ) $n_0>n$の場合
今までと固定端反射する位置はかわりません。
そのため、位相のズレも$π$のままです。
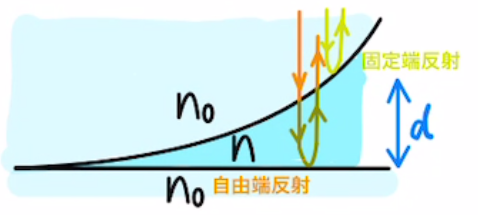
(ⅱ) $n_0<n$の場合
今までと固定端反射する位置は入れ替わります。
そのため、位相のズレは$-π$になるのですが、半周期ズレであることには変わらず、干渉縞の結果は (ⅰ) と同様です。
液体中では波長が$ \frac{λ}{n} $のため、液体を入れた状態での強め合う条件は
$ r’=\sqrt{(m – \frac{1}{2} )R\frac{λ}{n}} $
となります。
そのため4番目の明線は
$ r’_4=\sqrt{ \frac{7}{2} R\frac{λ}{n}} $
となり、これが $ r_3=\sqrt{ \frac{5}{2} Rλ} $ と等しくなるため、
$n= \frac{7}{5} = 1.4$
(5)
反対側から光をあてた場合、黄色の直進する光と二回反射したオレンジ色の光の干渉となります。
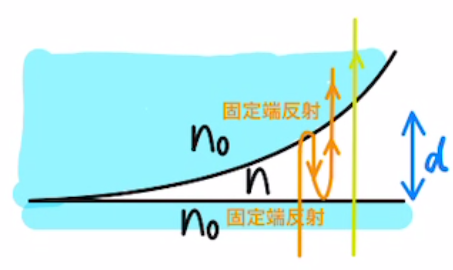
固定端反射のため、位相のズレは$2π$となり、さきほどとは明線と暗線の条件が逆になります。
つまり、弱めあう条件は
$ \frac{r^2}{R} = (m+\frac{1}{2})λ ⇒ r=\sqrt{ m + \frac{1}{2} Rλ}$
光が強め合う条件は
$ \frac{r^2}{R} = mλ ⇒ r=\sqrt{ mRλ}$
このことからニュートンリングは明暗が逆になったように見えます。