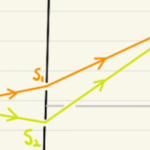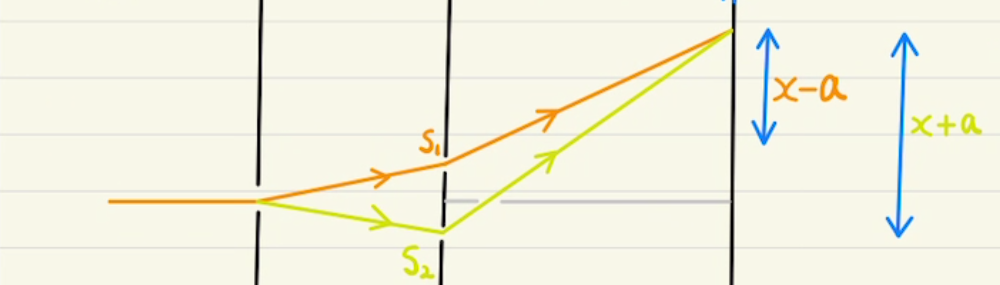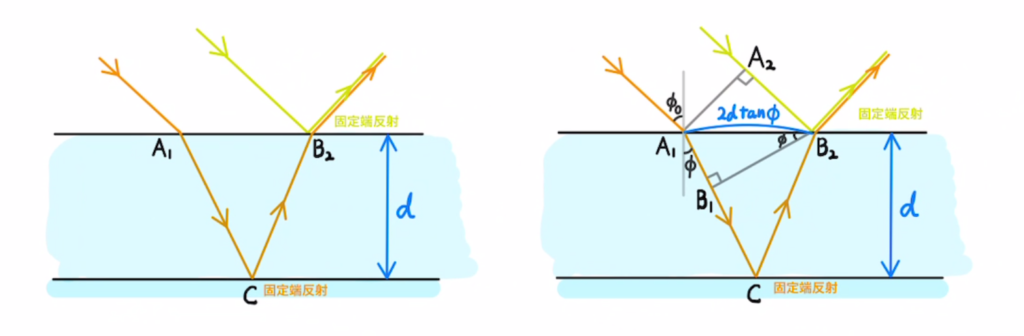
(1)$A_1B_1$と$A_2B_2$の光学的距離は等しくなるため、経路差は$B_1C+CB_2$となります。
実際、入射角を$Φ_0$、屈折角を$Φ$とすると、
$A_1B_1=2d\tan{Φ}×\sin{Φ_0}= 2d\tan{Φ}×n\sin{Φ} $
$A_2B_2=2d\tan{Φ}×\sin{Φ} $
から $1×A_1B_1 = n× A_2B_2 $がわかります。
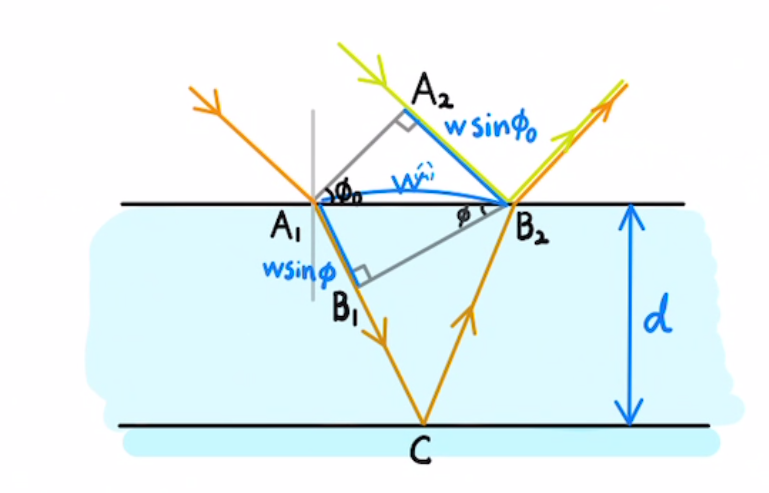
経路差$Δl$は
$B_1C+CB_2= (A_1C-A_1B_1)+CB_2 $
$=(\frac{d}{\cos{Φ}-2d\tan{Φ}sin{Φ}})+\frac{d}{\cos{Φ}}$
$= \frac{2d}{\cos{Φ}} (1-\sin^2{Φ}) $
$=2d\cos{Φ}$
となります。
(2)薄膜内での速度は$v_n=\frac{v}{n}= \frac{fλ}{n} $なので、
$λ_n=\frac{v_n}{f}= \frac{λ}{n} $
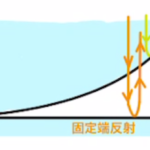
(3)$A_1$での反射は屈折率低→高であるため、固定端反射
$B_1$での反射も屈折率低→高であるため、固定端反射
つまり、反射による位相のズレは起こらない。
このことから、強め合う条件は
$mλ_n=2d\cos{ Φ }$
よって
$d=\frac{ mλ_n }{ 2\cos{ Φ } }= \frac{ m\frac{λ}{n} }{ 2\cos{ Φ } } $
$d=m× \frac{ λ }{ 2n\cos{ Φ } } $
(4)
さきほどの式に代入すると
$d=m× \frac{ λ }{ 2n\cos{ Φ } } = m× \frac{ 6.0×10^{-7}}{ 2×1.5\cos{60°} } $
$= 4.0×10^{-7} $
$m=1$の時に$d$が最小となるため、
$d_{min} = 4.0×10^{-7}[m]$
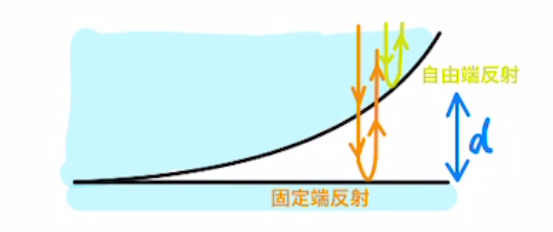
(5)$C$での反射では屈折率が高→低となり、自由端反射になる。
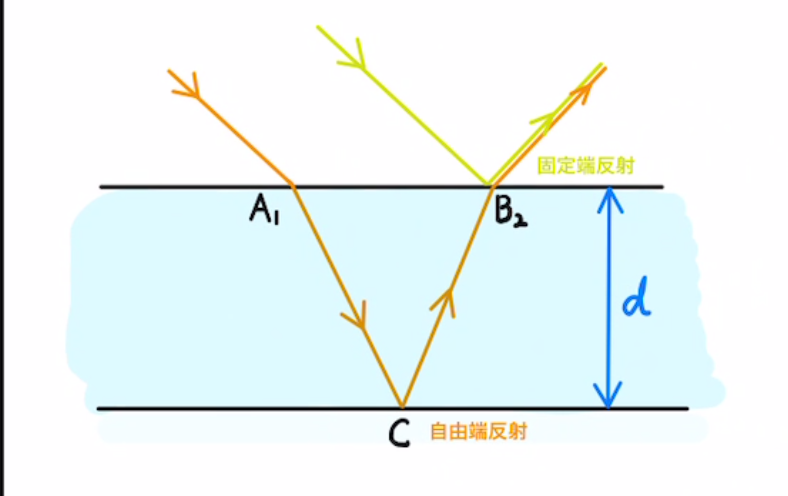
そのため、$B_2$で反射する光とは、位相が$π$ズレる。(半周期分)
つまり、強め合う条件は(3)の式よりも経路差$\frac{λ}{2}$分ズレて、
$ mλ_n=2d\cos{ Φ } + \frac{λ}{2} $
よって
$d=(m-\frac{1}{2})× \frac{ λ }{ 2n\cos{ Φ } } $
$m=1$のとき最小となるので、
$d_{min} = \frac{1}{2} × 4.0×10^{-7}[m] = 2.0×10^{-7}[m] $