回答欄
解説
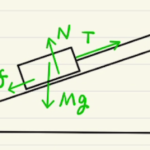
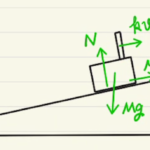
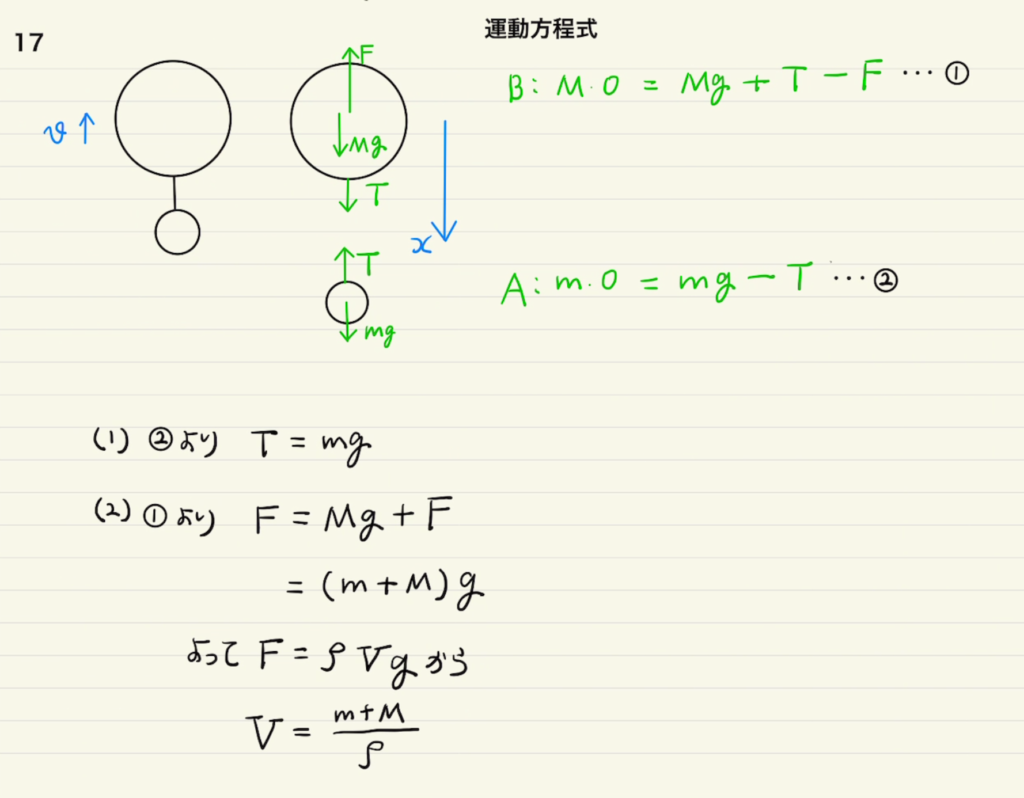
浮力を含めた運動方程式の問題ですね。浮力は同じ体積分の気体の重さ分($ρV$ $ρ$:気体の密度、$V$:体積)で覚えておきましょう。
(厳密な証明は難しいですが、直方体の浮力に関しては簡単に証明できます。)
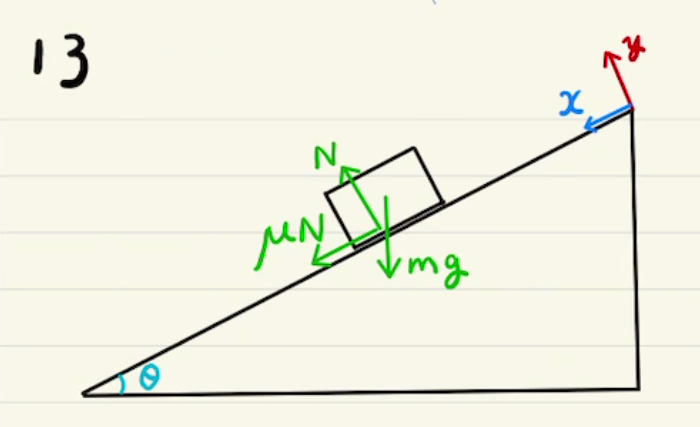
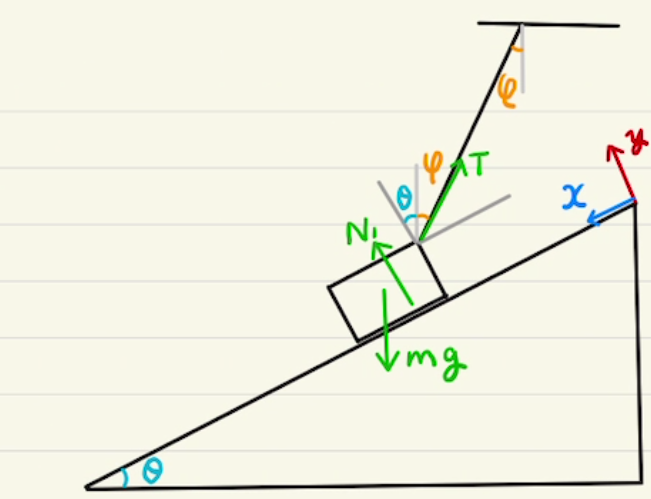
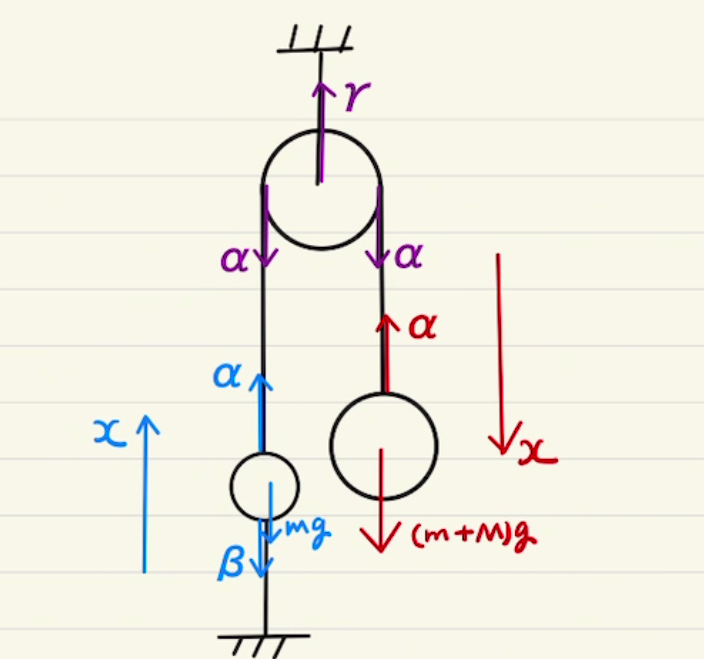
(1)(2)は静止状態の力のつり合い、(3)(4)は切り離した後の動きとなります。
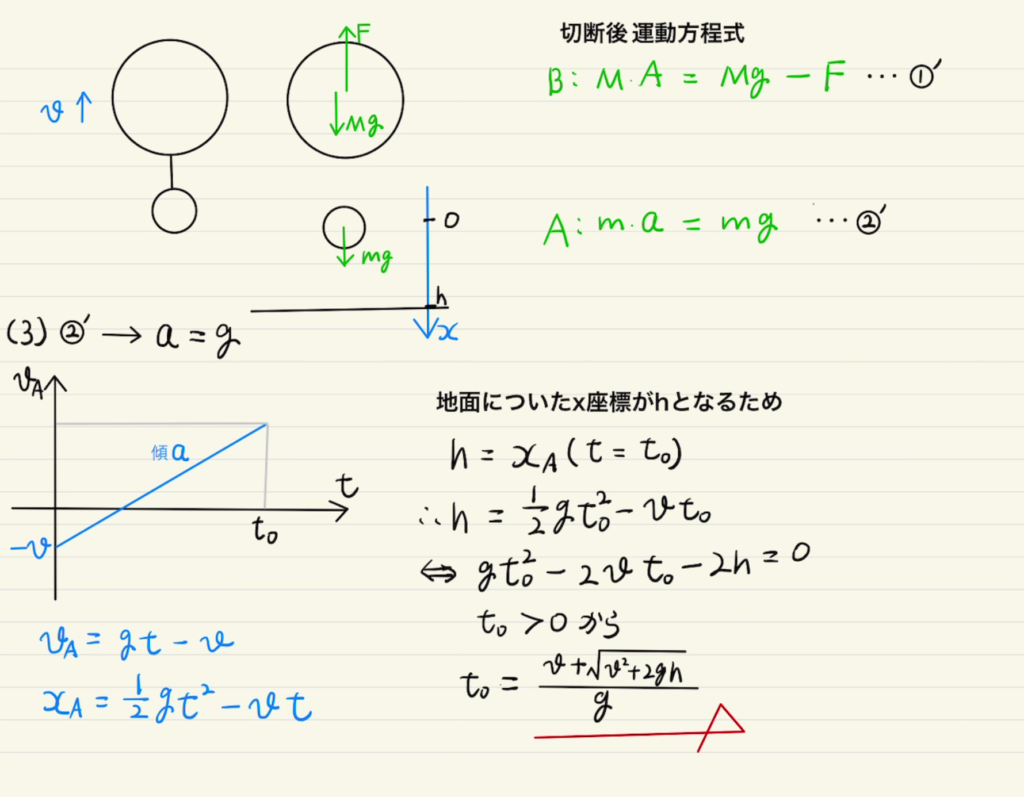
切り離す前は等速度で速度$v$となっているため、切り離した後の初速度は上方向に$v$であることに注意が必要です。
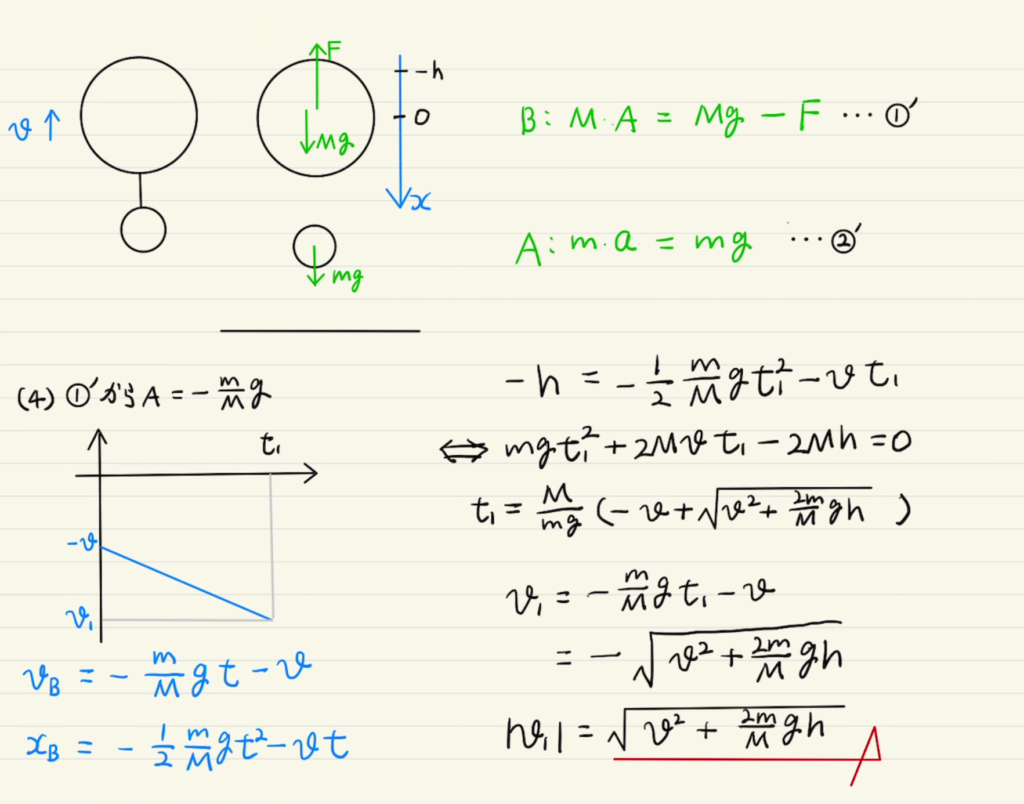
(3)(4)ともに加速度を二回積分して位置を$t$で表し、二次方程式を解くことになります。
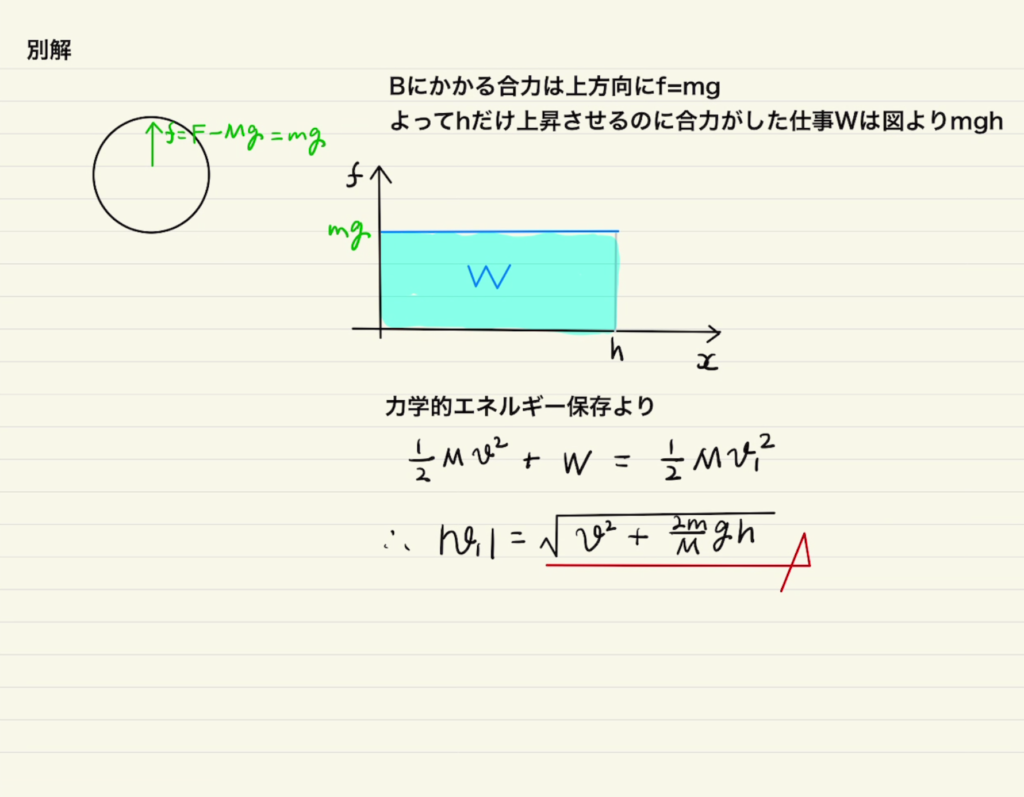
すでに力学的エネルギー保存の法則をやっていれば速度だけならすぐに求めることもできます。(習っていない方は次の範囲で出てきます。)
余談ですが$v_1^2 – v^2 = 2ah$という公式が解答に出てきますが、これは力学的エネルギー保存の書き換えですので覚える必要はないです。さらにいえば、使用できる条件が限られている(等加速度運動であるなど)ので混乱の元になるので推奨しません。
補足
(3)の積分がわかりにくければ、下のように面積で考えるといいでしょう。
$x$正方向に動いた距離(大きい三角)から、 $x$負方向に動いた距離(小さい三角) を引けばいいことになります。
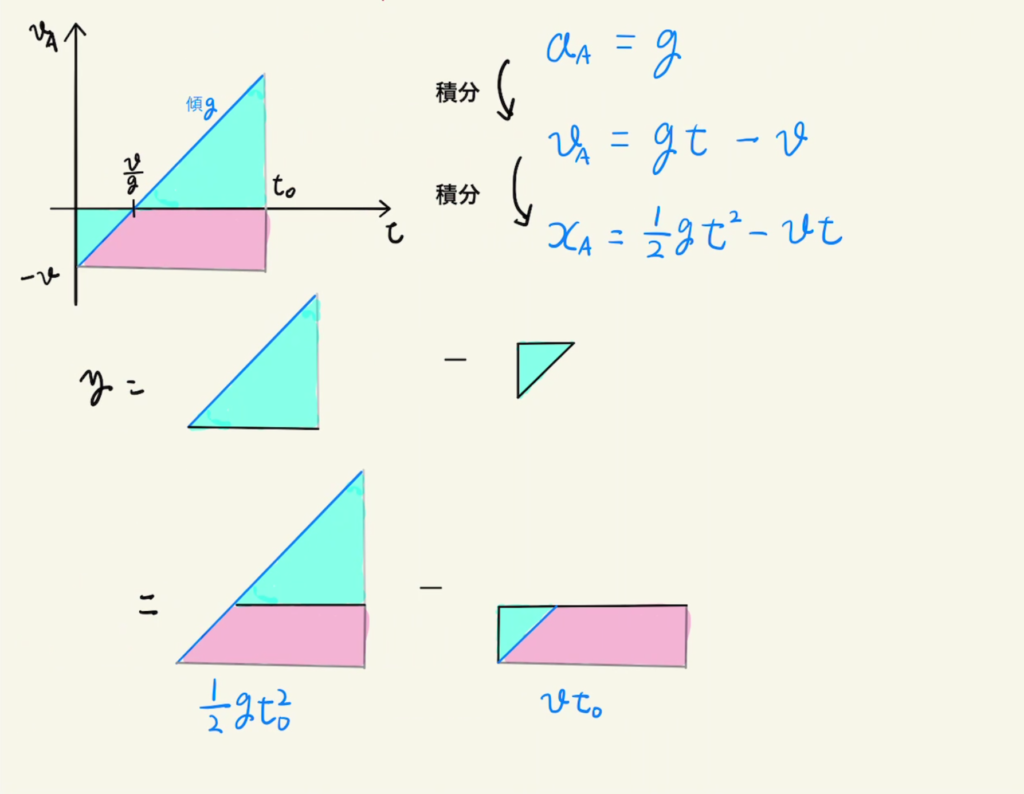
※解説だけなので問題は載せていません。参考書は自分で購入お願いします。