波の性質の所で波の式は下のように表せるとやりました。
$$ y( {\color{orange} t} , {\color{green} x}) = A\sin{2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})}$$
この波が二種類以上ぶつかり、波が強めあったり弱めあったりする現象を波の干渉といいます。
このとき注目するのが、位相 $θ = 2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ} ) $となります。
二つの光の位相が$Δθ$だけズレていたとすると、二つの波の方程式はそれぞれ下のように表せます。
$ y_1= A\sin{θ}$
$ y_2= A\sin{(θ+Δθ)}$
二つを足し合わせた波は
$ y = A\sin{θ} + A\sin{(θ+Δθ)} = 2A \sin{θ} \cos{ \frac{Δθ}{2} } $
・光が強めあう条件
$|\cos{ \frac{Δθ}{2} } |=1$となるとき、
$y = ±2A \sin{θ}$
となり振幅$2A$の波になります。
このとき光は強め合い、明るく見えます。
つまり、条件は $ \frac{Δθ}{2} = π×m$ なので、
$ Δθ = 2π×m$($m$は整数、m=…-1,0,1,2,3,…)
たしかに図に描いてみると、一周期分遅れれば全く同じ形の波になり、足し合わせると波が強め合いそうなのが確認できます。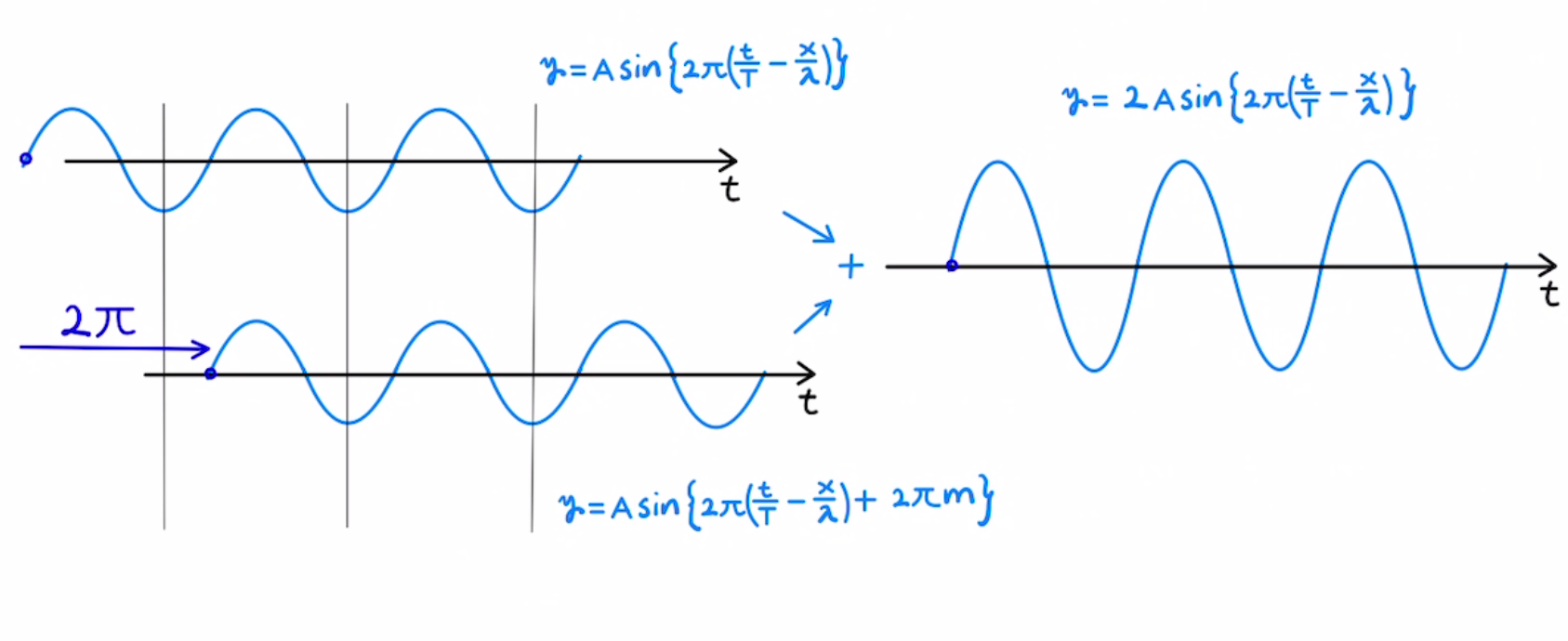
・光が弱めあう条件
$\cos{ \frac{Δθ}{2} } =0$となるとき、
$y = 0$
となり光は弱め合い、暗く見えます。
つまり、条件は $ \frac{Δθ}{2} = \frac{π}{2} + π×m$ なので、
$ Δθ = π + 2π×m$ ($m$は整数)
たしかに図に描いてみると、半周期分遅れれば逆向きの形の波になり、足し合わせると 波が弱め合いそうなのが確認できます。
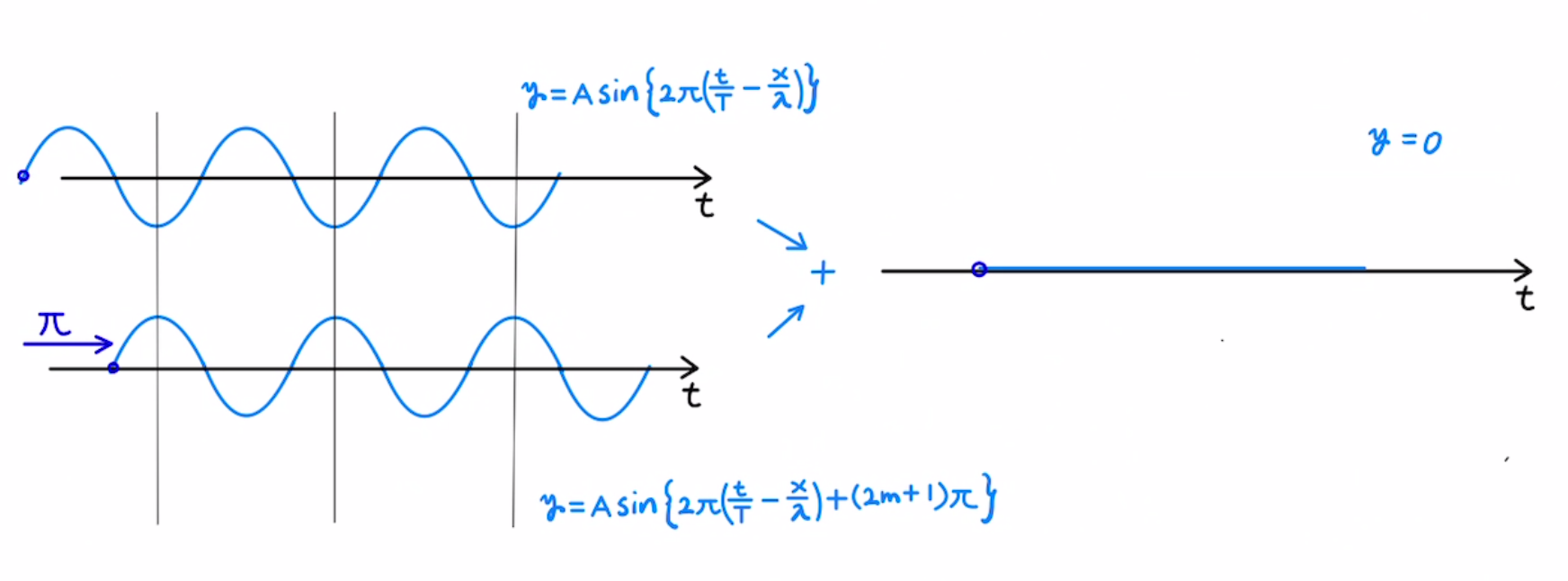
位相のズレ
位相のズレは主に二つの要因によって起こります。
それは経路差と固定端反射です。
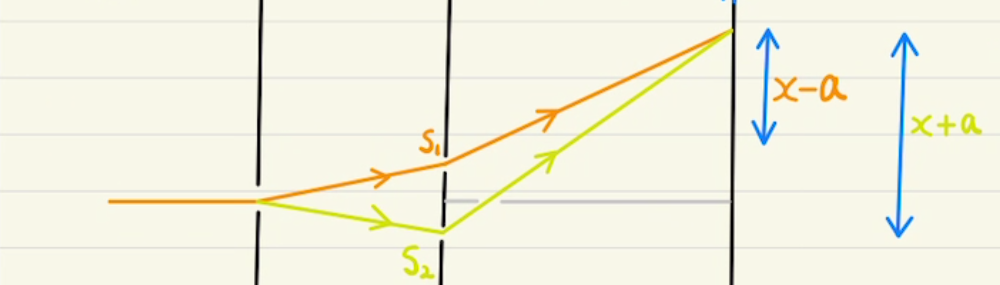
・経路差
二つの光が違う距離進むことで位相に差が生まれます。
具体的に移動した距離の差を$Δl$としましょう。
このとき位相の差$Δθ$は
$Δθ = 2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} (x+Δl)} }{λ} ) – 2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ} ) $
となり、
$Δθ = 2π\frac{Δl}{λ}$とわかります。
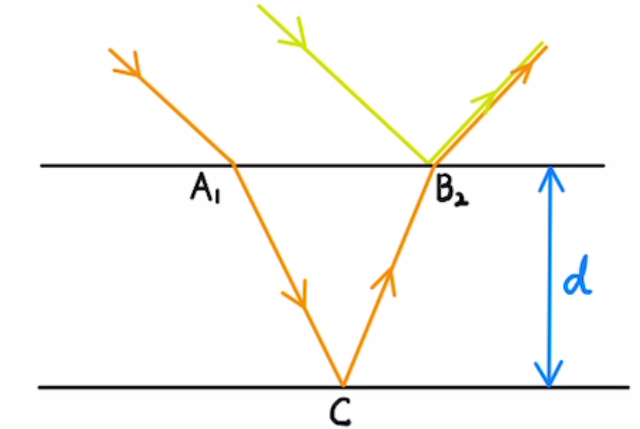
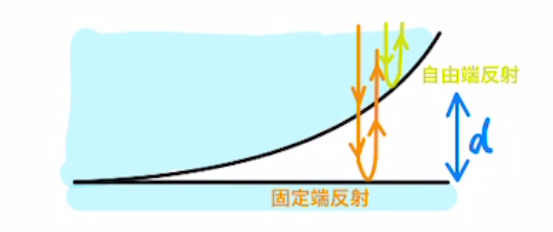
・固定端反射
光の反射にも自由端反射と固定端反射があります。
屈折率が高→低で反射する場合は、 自由端反射となり、位相の変化はありません。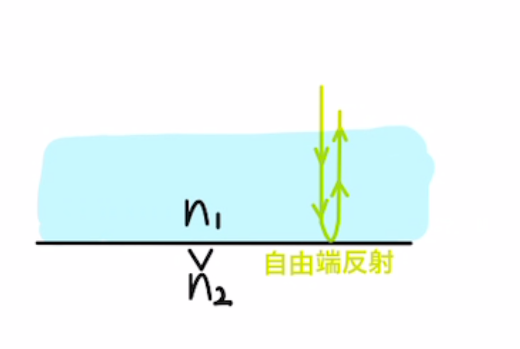
屈折率が低→高で反射する場合は、 固定端反射となり、位相はπだけズレます。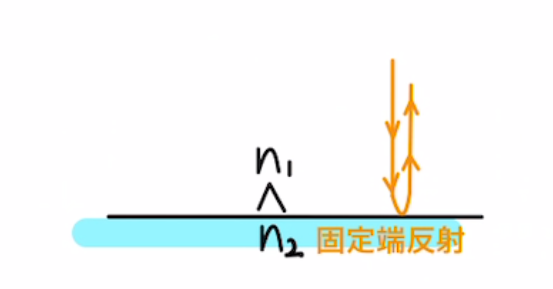
光1の固定端反射の回数を$N_1$回、光2の固定端反射の回数を$N_2$回とすると
位相差$Δθ$は
$Δθ = 2π\frac{Δl}{λ} + (N_2-N_1)π$
となり、これが $2π×m$なら強めあい、$π + 2π×m$なら弱めあうことになります。
この両辺を$\frac{λ}{2π}$かけて、以下のように書くこともできます。
(ⅰ)固定端反射の回数が偶数の場合
明るくなる条件: $Δl = mλ $
暗くなる条件 :$Δl = (m + \frac{1}{2})λ $
(ⅱ)固定端反射の回数が奇数の場合
明るくなる条件: $Δl = (m + \frac{1}{2})λ $
暗くなる条件 :$Δl = mλ $
まとめ
移動した経路差を$Δl$、以下のような条件で干渉が起こる
(ⅰ)固定端反射の回数が偶数の場合
明るくなる条件:$ Δl = mλ $
暗くなる条件 :$Δl = (m + \frac{1}{2})λ $
(ⅱ)固定端反射の回数が奇数の場合
明るくなる条件:$ Δl = (m + \frac{1}{2})λ $
暗くなる条件 :$Δl = mλ $