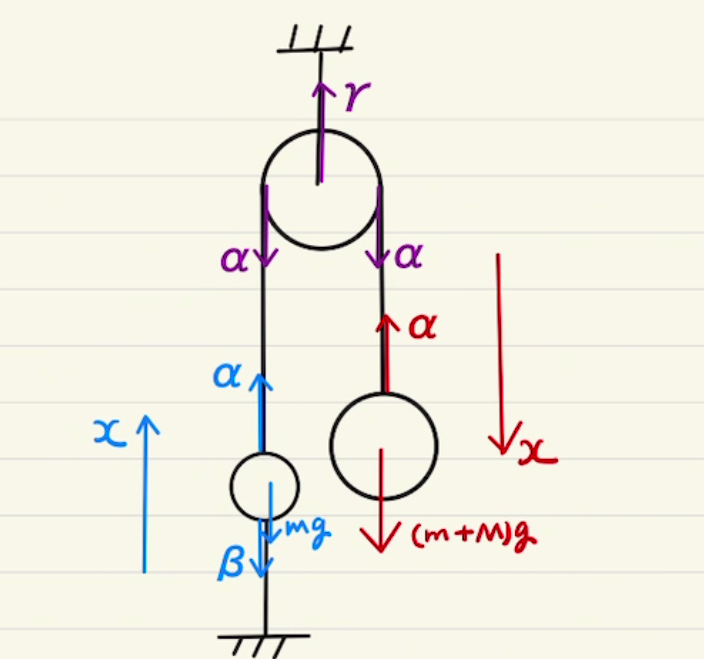
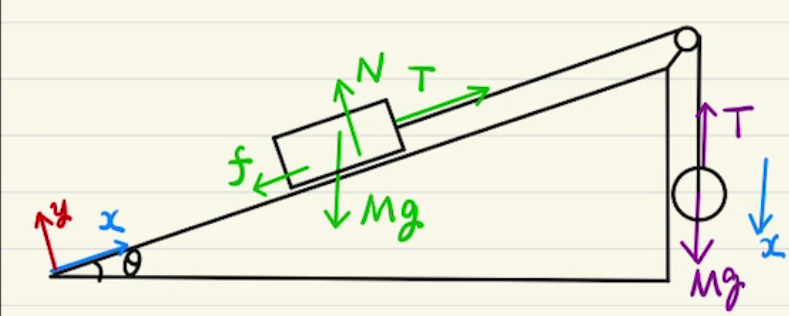
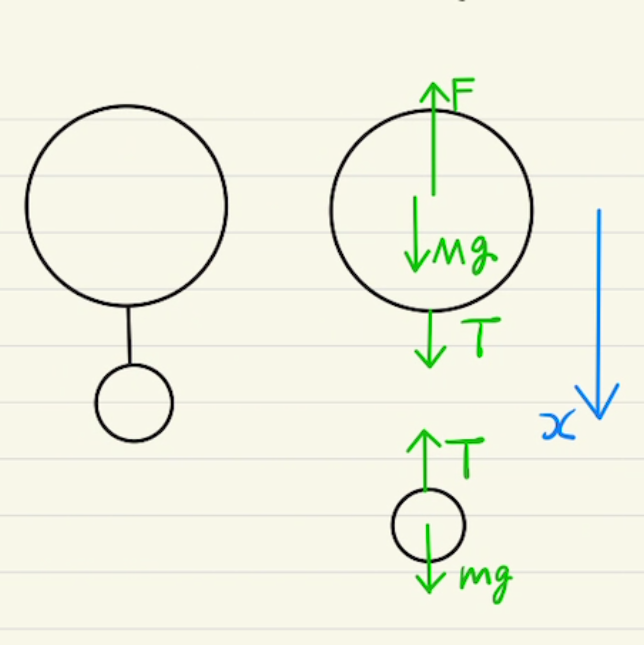
解答欄

解説
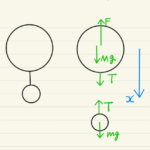
今回は空気抵抗の話になります。高校範囲で答えられる部分は限られるので、あまり多くは見かけません。
今までの問題とは違い加速度は一定ではなくなるため注意してください。
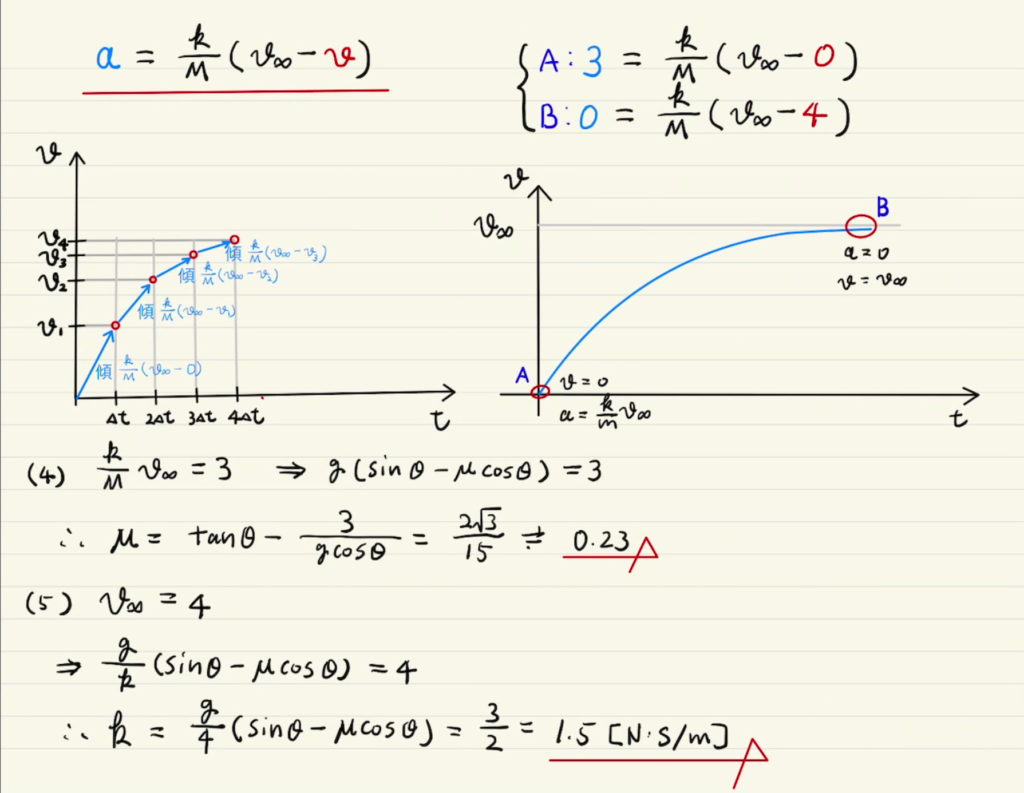
運動方程式からa=…の形にすると右辺にvがつくため複雑な動きをします。
具体的には二枚目左のグラフのように速度が上がるごとに加速度が下がる(傾きがゆるやかになる)。
それをつなぎ合わせると右のグラフのようになります。
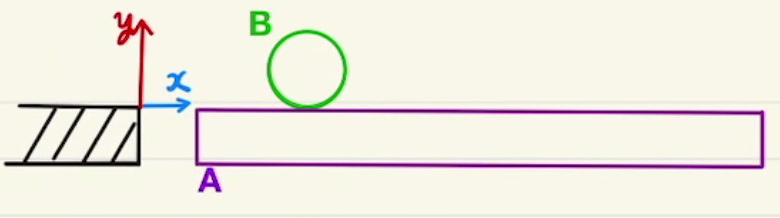
グラフ全体を関数として表すには難しいため、ほとんどの場合は最初(A)と最後(B)だけを見ることになります。
Aでは速度が0、Bでは加速度が0となります。
Aでの加速度もグラフの傾きからわかります。
Bでは加速度が0となるため速度が一定であり、これを終端速度と言います。今回は v∞ として表記します。
補足
高校の範囲外ではあるが微分方程式から計算をすることによって速度を時間の関数として表すことができます。
空気抵抗がある場合は指数関数となります。
たしかに$t=0$で$v=0$、$t→∞$で$v=v_∞$となることが確認できます。
また、それを積分して位置を求めることもできます。
先ほどの運動方程式の加速度$a$は速度を時間微分した$\frac{d{\color{blue} v}}{dt} $とあらわせることから、下の式で書けます。
$\frac{d{\color{blue} v}}{dt}=-\frac{k}{m}( {\color{blue} v} -v_∞) $
これを変数分離する。($v$と$t$を左辺と右辺に分ける。今回は$t$の変数を含まないので無視。)して
$\frac{d{\color{blue} v}(t)}{ {\color{blue} v} – v_∞ }=-\frac{k}{m}dt $
両辺を積分すると
$\log{( {\color{blue} v} – v_∞ )} = -\frac{k}{m}t + C $
となります。Cは積分定数なのであとで初速度から求めることができます。
今回は$e^{右辺}= e^{左辺} $とすることで
${\color{blue} v} – v_∞ = e^{-\frac{k}{m}t + C }$
⇒$ {\color{blue} v}(t) = e^C×e^{ -\frac{k}{m}t } + v_∞ $
となります。
$t=0$の時、 $ {\color{blue} v}(t) = 0$から$e^C = -v_∞$がわかります。
よって求めるべき速度は
$$ {\color{blue} v}(t) = -v_∞e^{ -\frac{k}{m}t } + v_∞ $$
と時間の関数として表すことができました。
これを積分して
位置$ x(t) = \frac{k}{m} v_∞e^{ -\frac{k}{m}t } + v_∞t $
も求まります。(初期位置$x(0)=0$より積分定数も0となるため。)
先ほどの式を微分して
加速度 $ a(t) = \frac{k}{m} v_∞e^{ -\frac{k}{m}t } $
を導くこともできます。

※解説だけなので問題は載せていません。参考書は自分で購入お願いします。