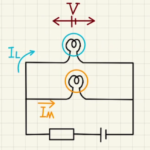
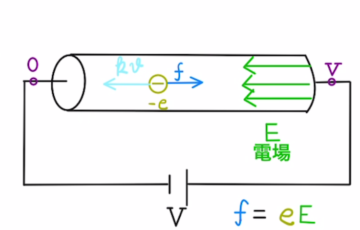
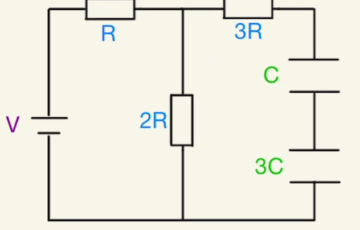
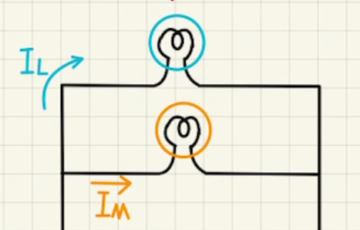
素直に毎回回路の方程式を立てていくのもありですが、電位差の比率で解けるものはそれを使ってもいいでしょう。
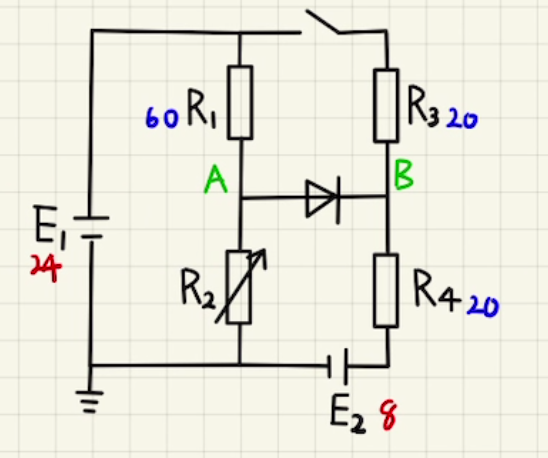
(1)
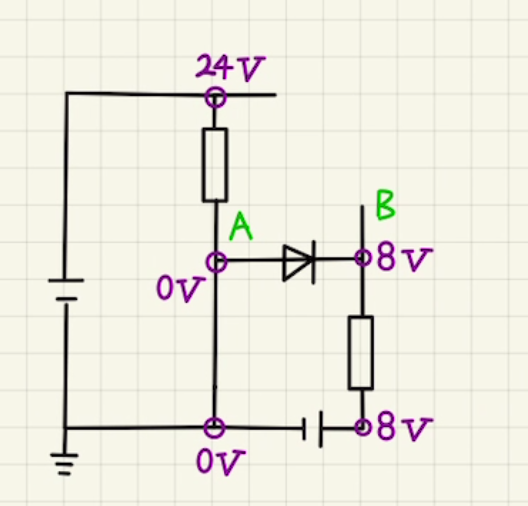
Aの方がBの電位が高いから。
Aは電位0[V]で
ダイオードは矢印の先端の方が電位が高い時は電流は流れません。
(2)
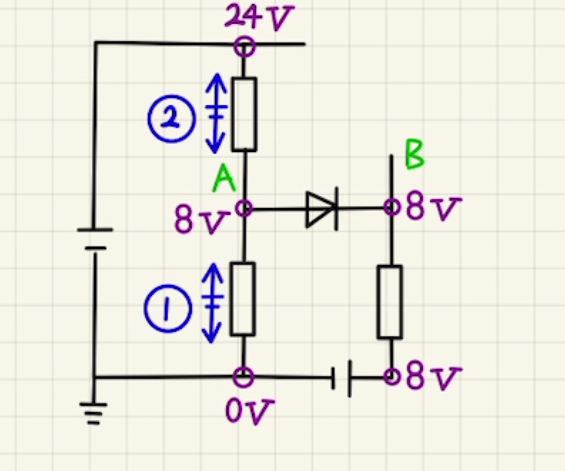
ダイオードに電流が流れていないとき、 $R_1$と$R_2$の電位差(電圧降下)の比は抵抗値と同じになります。
ダイオードに電流が流れないギリギリの$A$の電位が$B$と同じ8[V]になるときなので、このとき $R_1$と$R_2$の電位差は2:1となり抵抗値も2:1。
よって$R_2$は$R_1$の半分となり、$30[Ω] 答 $
(3)
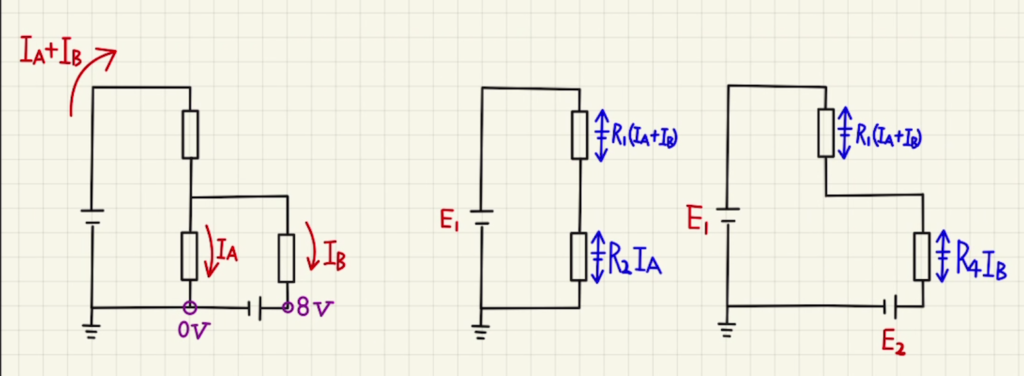
こちらはそのまま、二つの閉回路から連立する形になります。
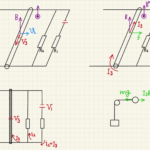
上の図のように流れる電流を$ I_A $, $ I_B $と置く回路の方程式は
\begin{cases}
& E_1 = R_1 (I_A+I_B) + R_2I_A \\
& E_1 = R_1 (I_A+I_B) + R_4I_B + E_2 \\
\end{cases}
それぞれの値を代入すると
\begin{cases}
& 24 = 60(I_A+I_B) + 60I_A ①\\
& 24 = 60(I_A+I_B) + 20I_B + 8 ② \\
\end{cases}
$2×②-①$より
$$I_B=\frac{8}{100}=8.0×10^{-2}[A] 答$$
(4)
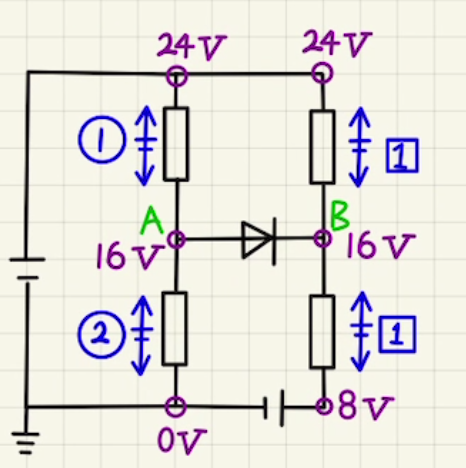
ダイオードに電流が流れていない状況を考えると、 $R_1$と$R_2$の電位差は抵抗値と同じ2:1となります。
よって$24[V]$と$8[V]$を1:1で内分した値がBの電位で$16[V]$となります。
電流がギリギリ流れないとき、Aの電位も$16[V]$のはずです。
そのため、 $R_1$と$R_2$の電位差は1:2となるため、抵抗値と同じ2:1となり、$R_2$は$R_1$の2倍の$120[Ω]$となります。
(Q)
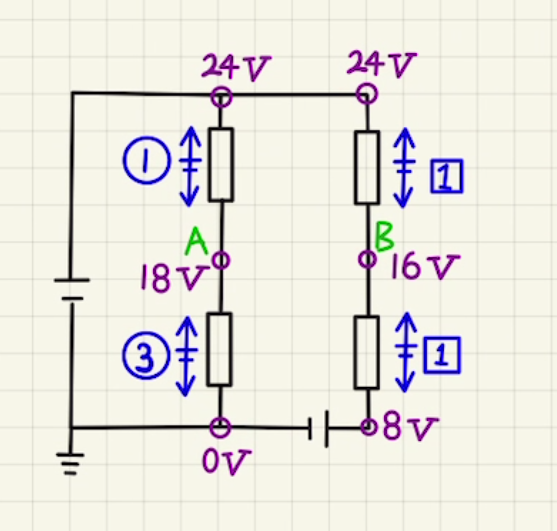
電流が流れない場合を考えると、 $R_1$と$R_2$の電位差は1:3となるためAの電圧は$18[V]$となりBの$16[V]$より電位が高くなって、電流が流れていないとおかしいことがわかります。
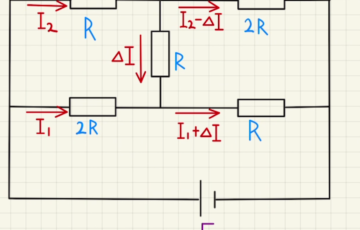
次に流れる電流について考えると、AとBの電位は等しいため、 $R_1$と$R_3$の電位差は等しく、流れる電流が抵抗値に反比例するため、図のような電流を考えることができます。
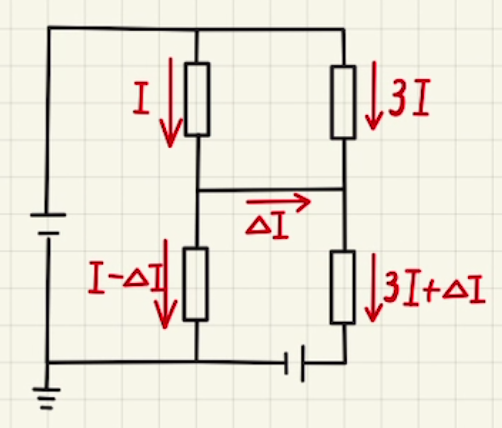
よって下の二つの回路から方程式を立てていきます。
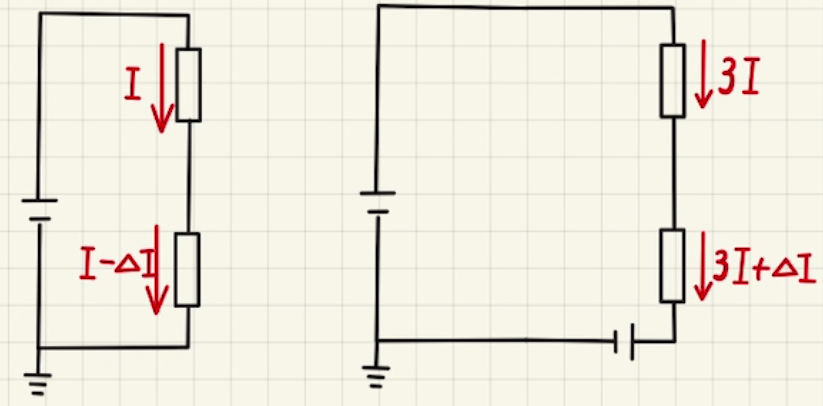
この回路の方程式はそれぞれ
\begin{cases}
& 24 = 60I + 180(I-ΔI) ③\\
& 24 = 20×3I + 20×(3I+ΔI) + 8 ④ \\
\end{cases}
$2×④-③$より
$$ΔI=\frac{2}{55}=3.6×10^{-2}$$