ミリカンの油滴実験 電子(電荷の最小単位)の存在を確認するための実験です。電子よりも小さい電荷は存在せず、電子の電荷$e$が最小となります。そのため電荷も電子何個分かで決まり、全ての電荷が$e$を整数倍したものになります…

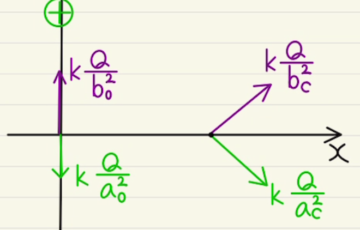
解答欄 解説 (1)(3)は電場とそれによってかかる力の問題となります。 電荷Aと電荷Bが発生させる二つの電場の足し合わせとなります。ただし、足し合わせと言ってもベクトルの足し合わせとなることに注意しましょう。点Oでは打…

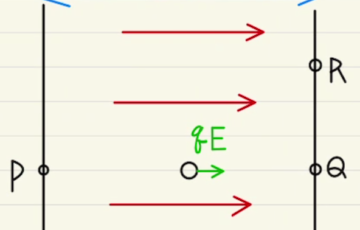
解答欄 解説 平行に一様な電場が発生している場合の問題となります。力に逆らって物体を動かすと位置エネルギーが上昇するように、電場に逆らって電荷を動かすと電位が上昇します。今回の場合は左側に行くほど電位が高くなっています。…

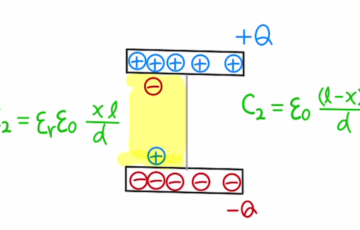
(1)(2)は定義に従った電気容量の問題となっています。コンデンサーの電気容量は$$C=ε\frac{S}{d}$$$ε$:誘電率,$S$:極板の面積:,$d$:極板同士の距離と定義されます。誘電率は真空の時は $ε_0…

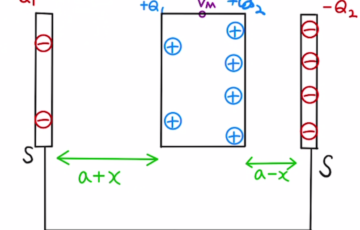
接地されている場所は電位$0$であることに留意します。(1)幅、面積が同じため、静電容量は等しくなります。両端の電位はどちらも$0$で電位差も等しくなり、どちらも$Q_0=CV_0$となり、合計は２Q_0となります。 孤…

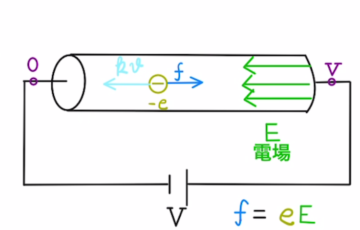
(1)抵抗の右端は電位Vで、左端は電位0となっています。抵抗の中では均一に電位が下がっていっているとすると、発生している電場は$$E=\frac{V}{l}$$となります。これは電場→重力、電位→位置エネルギーに置き換え…