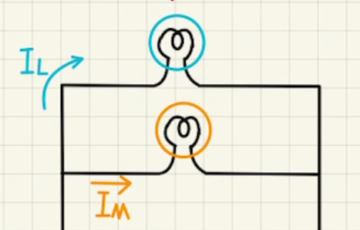
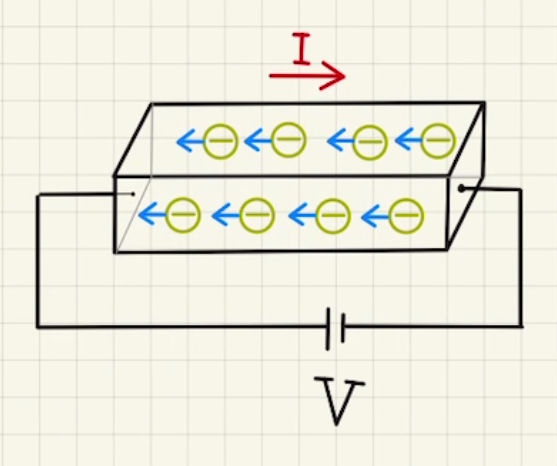
電流とは電荷が左から右へ川のようにながれていく現象です。
通常流れるのはマイナスの電荷である電子なので、電子が動く方向と電流の向きは正反対になります。
その動きを妨げるものを抵抗と言います。
基本事項
・ オームの法則
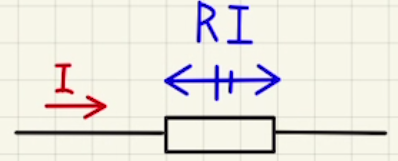
電流$I$が抵抗$R$に流れると、$RI$だけ電位が下がります。
・キルヒホッフ第一法則
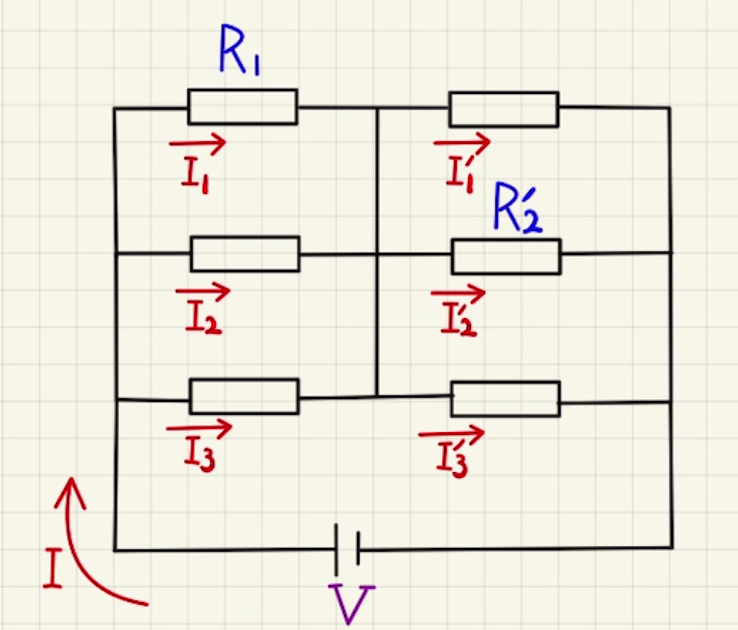
電流が分岐したとき時に、その電流は全て足し合わせになります。
$$I=I_1+I_2+I_3$$
・ キルヒホッフ第二法則
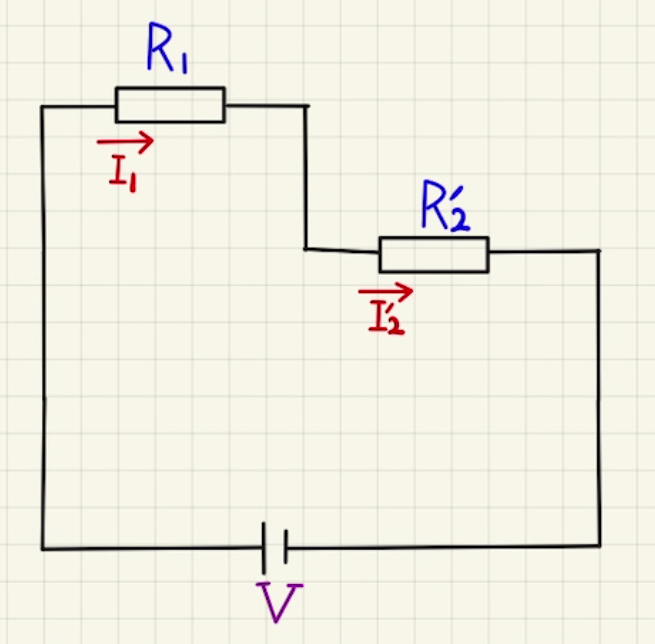
電流が一周すると、どの一周をとっても電位が元に戻ります。
つまり、かけた電圧は電圧降下の合計と等しくなります。
$$V=R_1I_1+R’_2I’_2$$
合成抵抗
条件を満たすとき、複数の抵抗を、あたかも一つの抵抗のように扱えます。
・直列
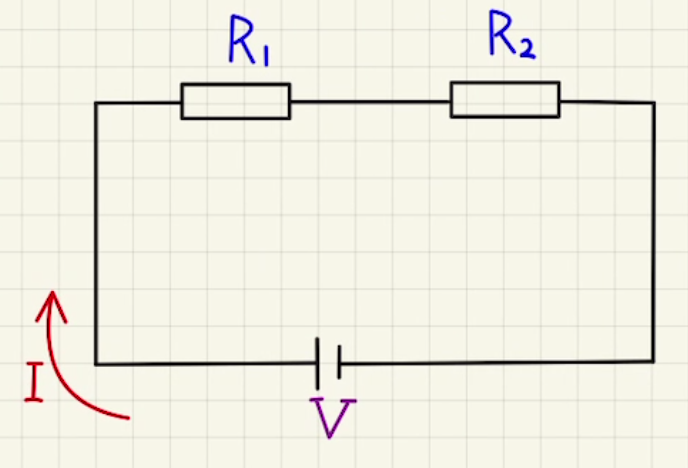
同じ電流が流れる二つの抵抗が直列で並んでいるとき、
\begin{align}
V&=R_1I+R_2I\\
&= (R_1+R_2)I \\
\end{align}
よって合成抵抗$R$は
$$ R = R_1+R_2 $$
・並列
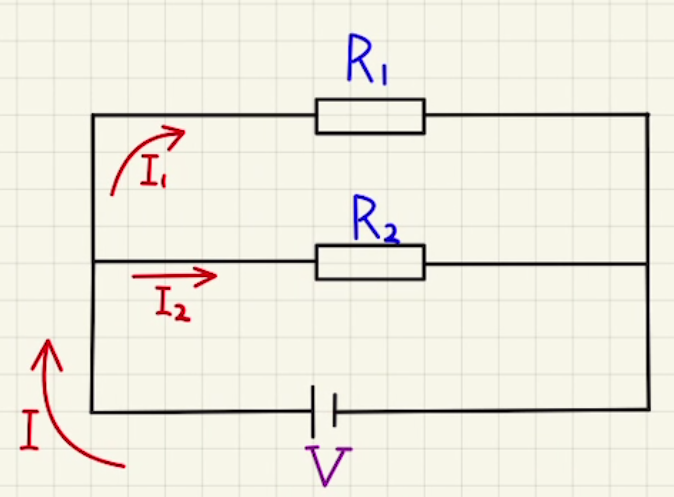
同じ電圧がかかる二つの抵抗が並列で並んでいるとき 、
\begin{align}
I&=\frac{V}{R_1}+ \frac{V}{R_2} \\
&= \left(\frac{1}{R_1}+ \frac{1}{R_2}\right)V \\
\end{align}
よって合成抵抗$R$は
$$ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} $$
と表せます。
※注
同じ電圧や同じ電流と言った前提条件を満たさない場合、合成抵抗として扱うことができません。
その場合、キルヒホッフの法則から連立して求めましょう。
・ホイートストンブリッジ
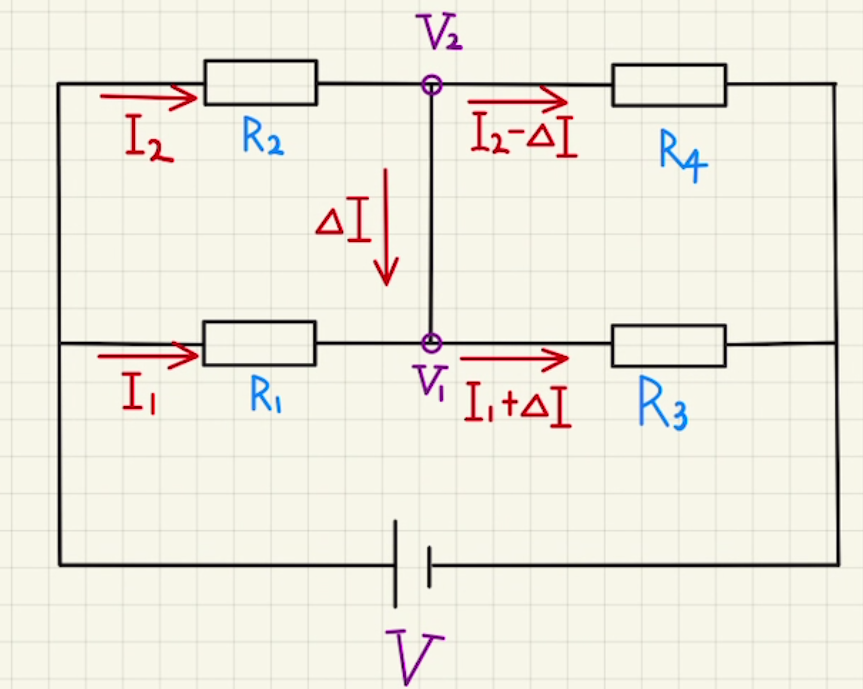
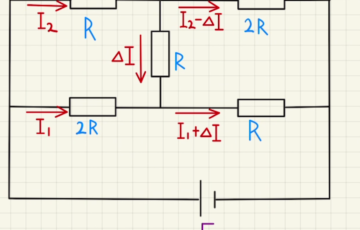
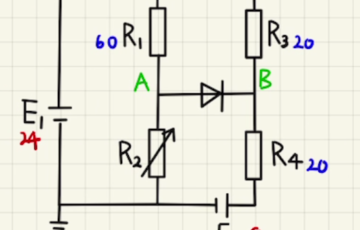
図のような回路をホイートストンブリッジといいます。
このような回路の場合、基本的に回路の合成を行っていくことはできません。
ただし、抵抗の比が$R_1:R_3=R_2:R_4$となると$V_1$と$V_2$が等しくなり、間に流れる電流$ΔI$は$0$になります。
これは間($ΔI$が流れる線)に起電力を持たないパーツ(抵抗や電流計、電荷を溜めてないコンデンサー等)を入れても変わりません。
逆に$R_1:R_3=R_2:R_4$の比が成り立たないときはキルヒホッフの法則を連立してそれぞれ電流電圧を求めていくしかありません。
電気抵抗内の電子
長さ$l$、断面積$S$の抵抗を考えます。
・電流

抵抗の中で動ける自由電子の数か、$1[m^3]$あたり$n$個とします。
そうすると、時間$t$秒の間に断面$S$を通る電子の数は
$$N=n(vtS)$$
となります。
電子一つあたり$-e$の電荷を持つため、その電荷の総量は
$$|Q|=e N= en(vtS) $$
これが時間$t$秒で断面を通る電荷の数で、この1秒当たりの電荷移動量を電流と言います。
つまり、
$$I=\frac{|Q|}{t}=enSv$$
・抵抗値と抵抗率
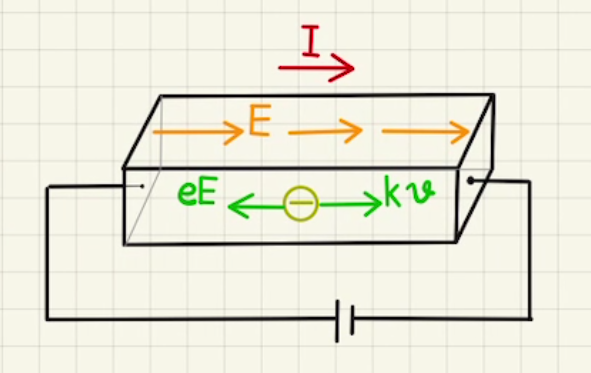
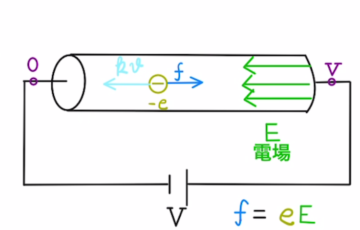
電子の速度に比例して、抵抗内では速度の反対側に力を受けます。空気抵抗みたいなものですね。
この抵抗力を$kv$とおきます。
電流が安定しているとき抵抗内の電場は$E$ による力と、抵抗力がつり合っています。
力のつり合いは
$$e E =kv$$
よって速度は
$v =\frac{eE}{k} =\frac{eV}{kl}$となることがわかり、
電流の値に代入すると、
$I=enS\frac{eV}{kl} $
となります。
よって抵抗値は
$$R=\frac{V}{I}= \frac{k}{en^2} \frac{l}{S} $$
と計算することができました。
抵抗は断面積に反比例し、長さに比例することがわかります。
この$ρ= \frac{k}{en^2}$を抵抗率といい、素材によって決まります。
$$R=\frac{V}{I}=ρ\frac{S}{l} $$
・抵抗の消費電力
抵抗の全ての自由電子の数$N_a$は
$N_a=n(Sl)$となります。
これらの電子は全て電場による力$eE$がかかっています。
この力の合計は
$$F=N_aeE= nSle\frac{V}{I} =enSV$$
この力がt秒間に動かした距離は$vt$となるため、電場が抵抗にした仕事は
$$W=F・vt= \frac{e^2nS}{kl}V^2t= \frac{V^2}{R}t$$
となります。
これは電池によって作られた電場が抵抗でした仕事となります。
つまり、電池が電場を作る→電場が電子の流れさせる→電子が抵抗で衝突→分子の熱振動を増やす→外に放出、という流れになります。
電場がした仕事はそのまま抵抗で消費されます。
このことから、抵抗で1秒あたりに消費された仕事は
$$ P=\frac{V^2}{R}=RI^2 $$
となることを確認できました。
直流回路によく使われるパーツ
・電池
一定の起電力で電荷を押し出そうとする。
Vの起電力で電荷$Q$だけ移動させると、した仕事は$QV$となる。
そのため、1秒当たりに電池がする仕事は$P=\frac{d}{dt}(QV)=IV$
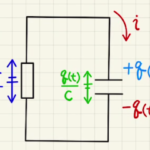
・コンデンサー
たまっている電荷が$Q$のコンデンサーは電位差が$V_C=\frac{Q}{C}$となります。
電荷の出入りが電流となるため、
$$I=\frac{dQ}{dt}$$が使えます。
・ダイオード
AからB方向にしか電流を流すことができません。
回路の中で考えるときは、実際に流れない想定で電位差を計算し、Aの電位がBよりも高ければ電流が流れると言えます。
・非線形抵抗
抵抗値が一定値とならないため、$V=RI$を使えない抵抗を言います。
$V$と$I$の関係は綺麗な関数で表せないことが多く、一般的にはグラフから判断します。
回路の方程式から求めた、 $V$と$I$の関係をグラフに書き込み交点から求めるのが一般的です。
抵抗の温度により$R(T)=\frac{V}{I}$が変わります。
非線形抵抗の温度係数$α$は「温度が1℃変化したときの抵抗値の変化割合」です。
例えば、常温から温度が1℃上がったら抵抗値が0.1%上がった場合、$α=0.1×10^{-2}$となります。
常温で$R_0=1000[Ω]$の抵抗だった場合、1℃上がるごとに$αR_0=1[Ω]$ずつあがっていくことがわかりますね。
室温$T_0$の抵抗値を$R_0$とすると、温度$T$のときの抵抗値は以下のように表せます。
$$R(T)= R_0 + αR_0(T-T_0)$$
電流計と電圧計
流れている電流を計測する機器を電流計、ある区間の電位差を計測するものを電圧計といいます。
・電流計
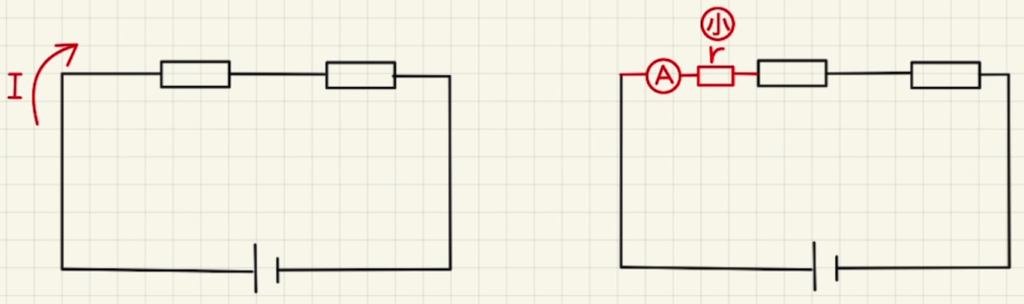
電流を計測したい場所に直列で電流計をつなぎます。
もし内部抵抗$r$が大きいと電流計がないときより流れる電流が小さくなってしまいます。
そのため内部抵抗値は極端に小さいほうが好ましいです。
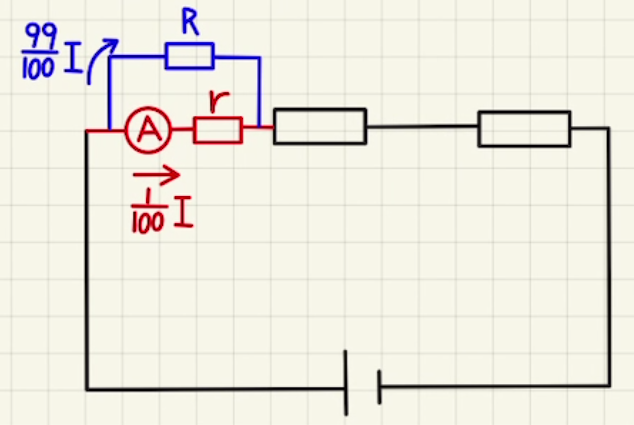
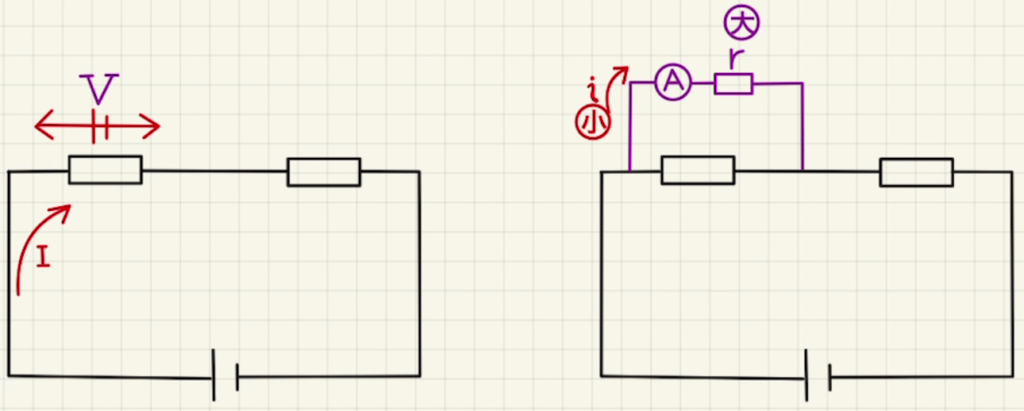
測れる電流をより大きくしたい場合は並列に抵抗をつなぎます。
例えば並列に並べた抵抗$R$が内部抵抗$r$の$\frac{1}{99}$倍とした場合、電流計に流れる電流は$\frac{1}{100}$倍となります。
電流計の針が$1[mA]$をさしてるとき$I=100[mA]$、針が$10[mA]$のときに$I=1000[mA]$などとわかります。
・電圧計
電位差を計測したい場合、並列で電圧計を並べます。
電圧計と言っても計測するのは電流になります。内部抵抗がわかっていれば$V=RI$から電圧を求めることができます。
もし電圧計に多くの電流が流れてしまうと、電圧計がないときより電位差が小さくなってしまいます。
そのため、内部抵抗値が極端に大きいほうが望ましいです。
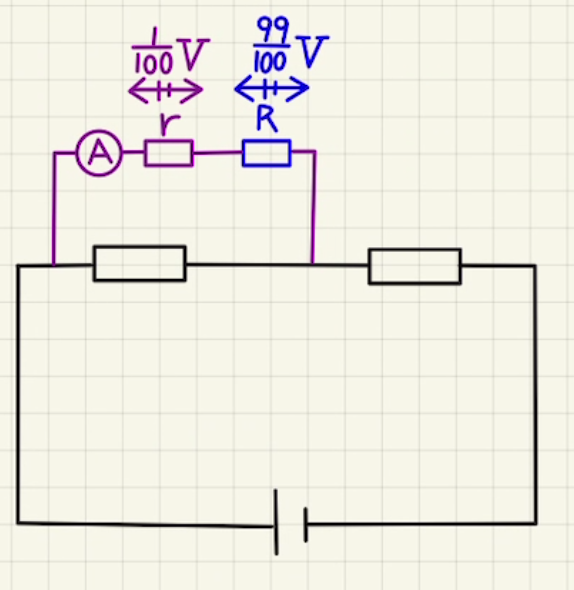
測れる電圧を大きくしたい場合は直列で抵抗をつなげます。
例えば並列に並べた抵抗$R$が内部抵抗$r$の$99$倍とした場合、内部抵抗の電位差は$\frac{1}{100}$倍となります。
そのため、電圧計の針が$1[V]$をさしてるとき$V=100[V]$、針が$10[V]$のときに$V=1000[V]$などとわかります。