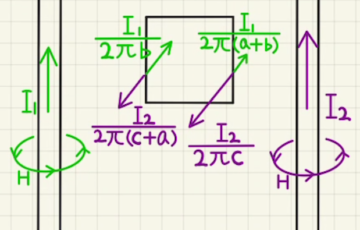
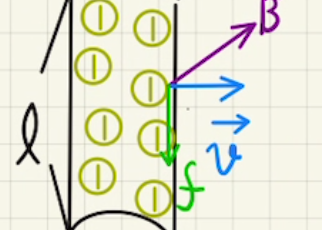
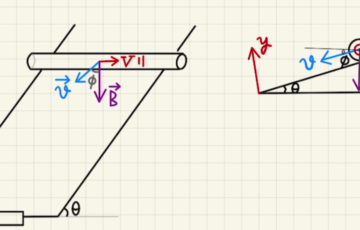
電流や磁場の関係則の背景にはアンペールの法則とビオサバールの法則というものがあります。
式として違うこの二つの法則は本質的には同じで、状況によって使い分けていくことになります。
今回はこの二つについて見ていきましょう。
アンペールの法則
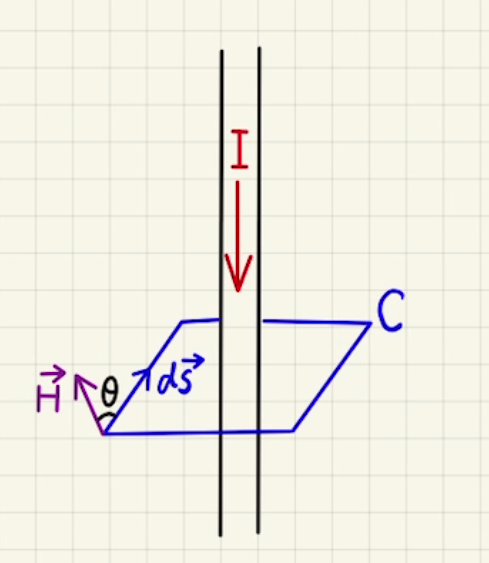
アンペールの法則は流れる電流とその周りに流れている磁場の関係の式です。
$$I=\int_C{\vec{H}d\vec{s}}$$
これはなにを意味しているかを考えるために、電流のまわりをある経路を一周ぐるっと回る経路を考えます。この一周の線を$C$とします。
この一周はどんな形でもかまいません。
このとき、 $\vec{H}$と$d\vec{s}$のなす角を$θ$とすれば
$$I=\int_C{H\cos{θ}ds}$$
ざっくり言えば、経路全ての [磁場×長さ×$\cos{θ}$] を足し合わせたものと、電流が一致するということです。
ちなみに経路の内部に電流が複数流れている場合はその合計となります。
ビオ・サバールの法則
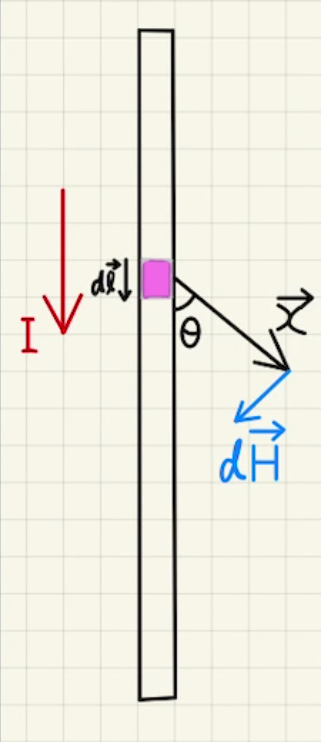
電流が流れているときに発生磁場が発生します。
ここでは、直線を流れる電流、円を流れる電流、ソレノイド・コイルについて扱います。
図のように電流$I$が流れているときに微小な長さに区切ってそれが発生させる磁場を見ます。
微小な長さを電流進行方向に$d\vec{l}$とすると、位置$x$で発生する磁場$d\vec{H}$は
$$d\vec{H}=\frac{1}{4π}\frac{I}{x^3} d\vec{l} × \vec{x} $$
となります。
このとき、$d\vec{l}$と$\vec{x}$のなす角を$θ$とすれば磁場の大きさ$dH$は
$$dH=\frac{1}{4π}\frac{I\sin{θ}}{x^2}dl$$
となり、方向は電流の右ネジの方向になります。
直線を流れる電流
・アンペールの法則
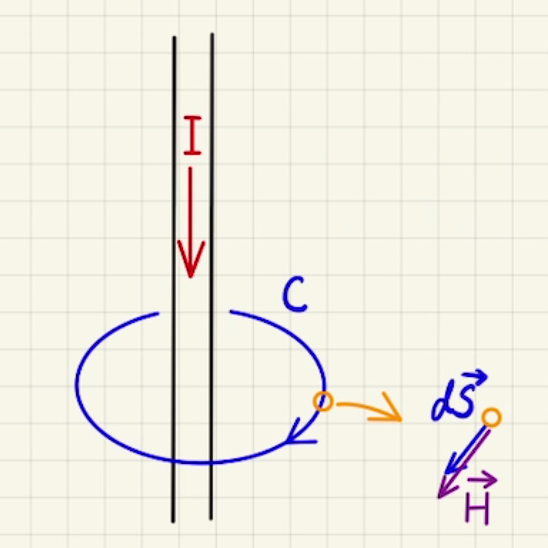
直線の周りを半径$r$の円形に沿った周回をする場合、常に経路と磁場が平行になるため$\cos{θ}$が1になります。
また、経路では常に磁場$H$であり、$\int_C{ds}$は一周の長さなので、
$$I=\int_C{H\cos{θ}ds}= H\int_C{ds}=H×2πr $$
このことから
$$H= \frac{I}{2πr} $$
が求まります。
・ビオサバールの法則
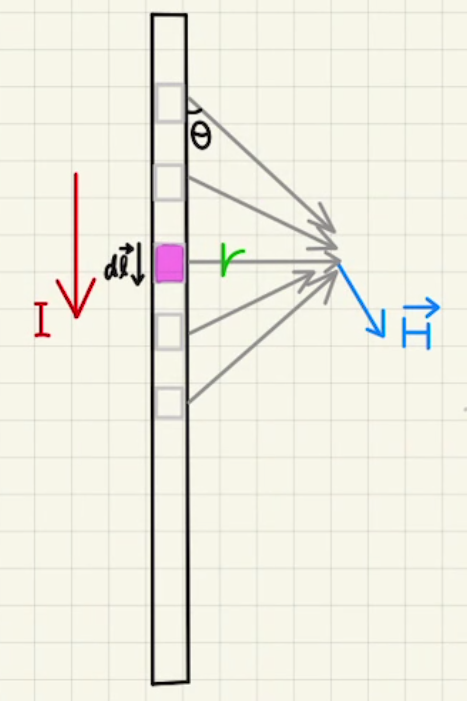
直線を流れる電流が、距離$r$だけ離れた場所に作る磁場を計算します。
直線は十分に長いとすると、電流が作る磁場$dH$は直線のどの位置でも発生させる磁場の向きは同じなので、全て足し合わせればよくなります。
\begin{align}
H&=\frac{I}{4π}\int_{-∞}^∞\frac{\sin{θ}}{x^2}dl \\
&=\frac{I}{4π}\int_0^π\frac{\sin{θ}}{r}dθ\\
&=\frac{I}{2πr}
\end{align}
(途中で-$l\tan{θ}=r$で$l$から$θ$に置換積分しています。)
よって直線に流れる電流が作る磁場は
$$ H=\frac{I}{2πr}$$
となります。
また、ベクトルで表記すると、
$$ \vec{H}=\frac{\vec{I}}{2πr}×\frac{\vec{r}}{r}$$
・円を流れる電流
・アンペールの法則
円形の場合、磁場の分布が変則的であるため、この法則を当てはめるのは困難です。
ビオサバールの法則の法則での説明だけにします。
・ビオサバールの法則
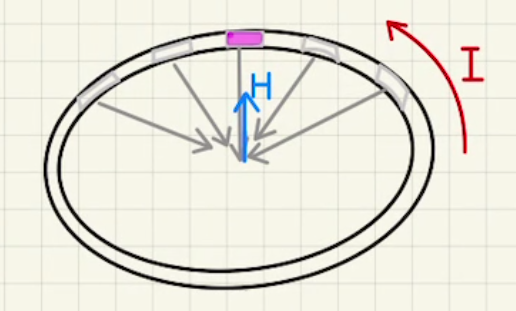
半径$r$の円を流れる電流が、中央に作る磁場を計算します。
円形なので電流方向$d\vec{l}$と、円中央までのベクトル$\vec{x}$は常に垂直です。
そのため、$ \sin{θ}=1 $となります。
また、$\vec{x}$の大きさも常に半径$r$で一定です。
このことから、
\begin{align}
H&=\frac{I}{4π}\int_C{\frac{\sin{θ}}{x^2}dl} \\
&=\frac{I}{4π}\frac{1}{r^2}・2πr\\
&=\frac{I}{2r}
\end{align}
よって直線に流れる電流が作る磁場は
$$ H=\frac{I}{2r}$$
となります。
また、向きは電流の右ネジ方向となります。
ソレノイド・コイルに流れる電流
ソレノイド・コイルとは筒状コイルのことで、単にソレノイドと呼ぶこともあります。
円形の電流では円の中心以外では磁場は変則的で、計算するのが困難でした。
そのため、その円形電流を重ね合わせたものはそのまま足し合わせて求めるのは難しそうです。
計算を簡単にするため、今回は理想的なソレノイド・コイルを想定します。
理想的とは、十分に長くコイルが十分に密に均質に巻かれている状態を指します。
・アンペールの法則
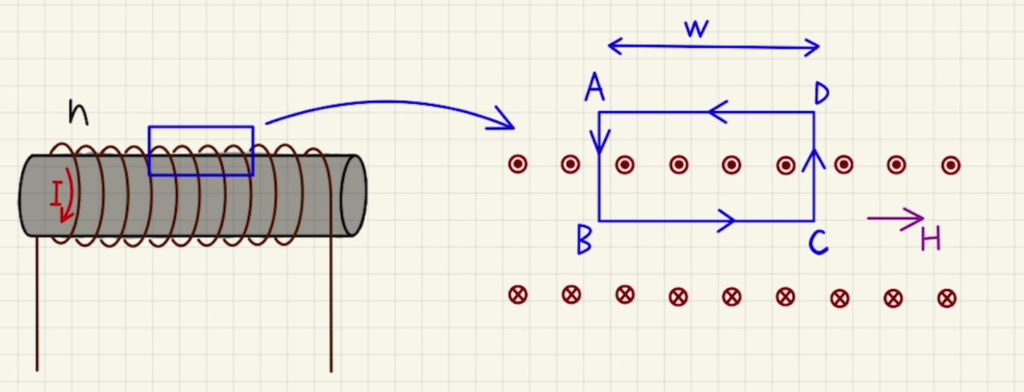
図のようにコイルを中央で切断して中と外を通る幅$w$の経路を考えます。
単位長さ当たりの巻き数を$n$とすると、$nw$だけの導線が通過します。
このことから周回内を通る電流の合計は
$$I=(nw)I$$
一方周回を通る磁場は$B→C$の時だけ磁場が進行方向に通っているため、
\begin{align}
\int_C{H\cos{θ}ds} &= \int_{A→B}{H\cos{θ}ds} + \int_{B→C}{H\cos{θ}ds} + \int_{C→D}{H\cos{θ}ds} + \int_{D→A}{H\cos{θ}ds} \\
&=0+0+H×w+0\\
&=Hw
\end{align}
よって、アンペールの法則から
$$(nw)I= Hw $$
となるため
$$ H= nI $$
・ビオサバールの法則
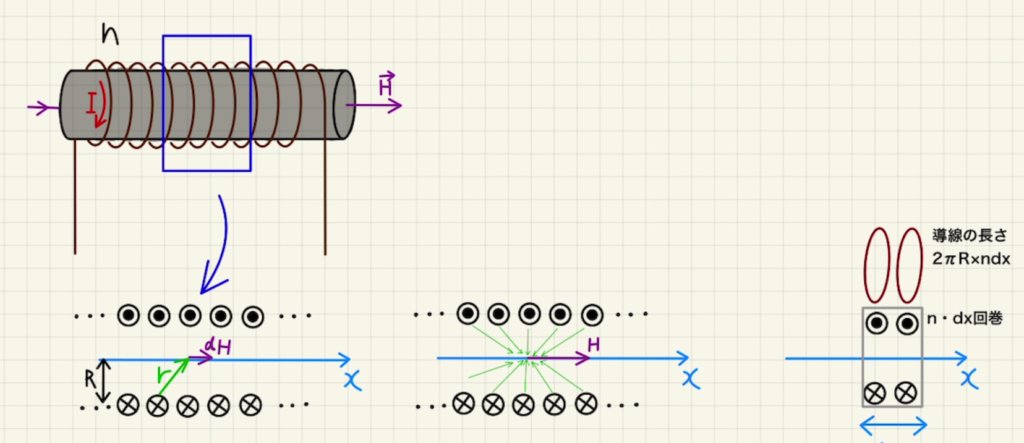
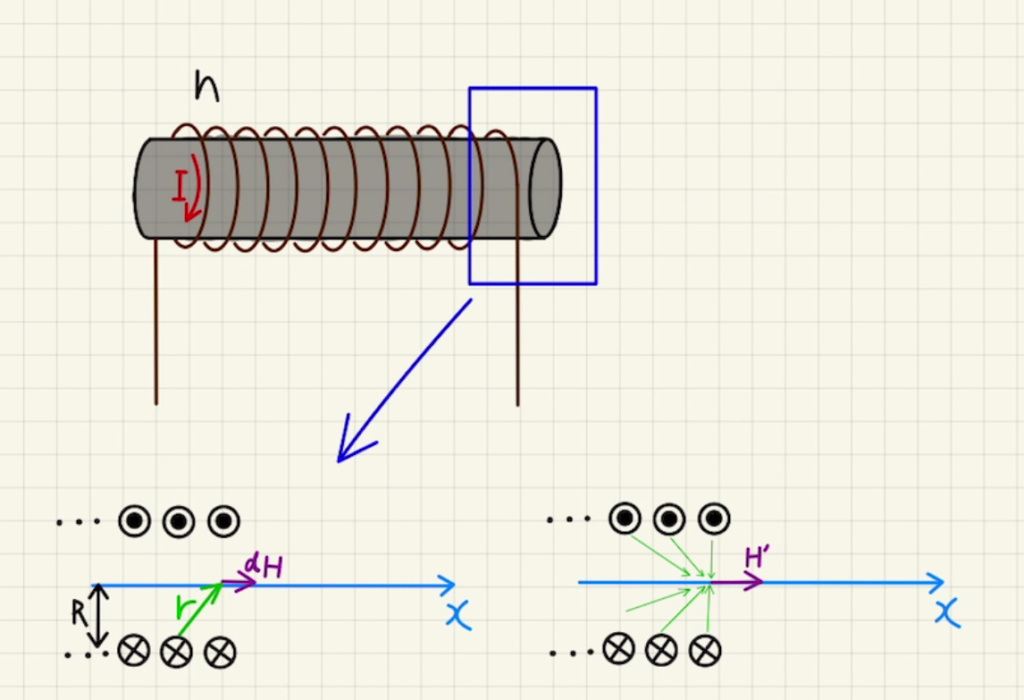
ソレノイド(筒状の)コイルを微小な長さに区切り、発生させる磁場を見てみます。
角度$\sin{θ}= \frac{R}{r} $となります。
また、縦に$dx$だけ切断すると、導線が$ndx$回巻だけ残ります。
よってその区間の導線は$2πR×ndx$の長さだけ残ります。
これらを代入すると
\begin{align}
dH&=\frac{I}{4π}\int_C{\frac{\sin{θ}}{x^2}dl}\\
&=\frac{I}{4π}\frac{\frac{R}{r}}{r^2}n・2πR\\
&=\frac{R^2nI}{2r^3}\\
&=\frac{R^2nI}{2(x+R)^{\frac{3}{2}}}
\end{align}
よって全ての電流がつくる電場は
\begin{align}
H&=\frac{R^2nI}{2}\int_{-∞}^∞{\frac{1}{ 2(x+R)^{\frac{3}{2}} }dx} \\
&=nI\\
\end{align}
※この結果は両端に十分な長さのコイルがある場所(中央付近)に当てはまります。
つまり、コイルの端では当てはまりません。
コイルの端では片側しかないため、
\begin{align}
H’&=\frac{R^2nI}{2}\int_{-∞}^0{\frac{1}{ 2(x+R)^{\frac{3}{2}} }dx} \\
&=\frac{1}{2}nI\\
\end{align}
と磁場が半分になります。