名問の森Ⅱ 46 解説

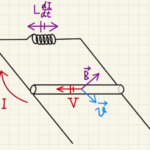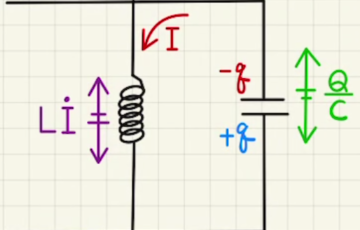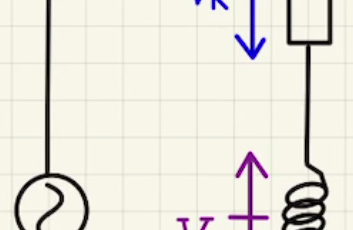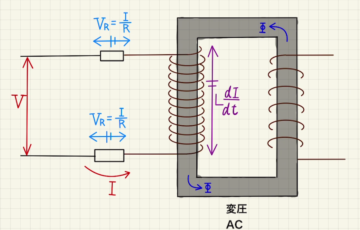
並べる順番が違えど、RLC並列回路で考えることはかわりません。
三つのうち一つに流れる電流がわかっているため、他に流れる電流は同じになります。
あとは、それぞれのパーツごとの電圧差を考えることになります。
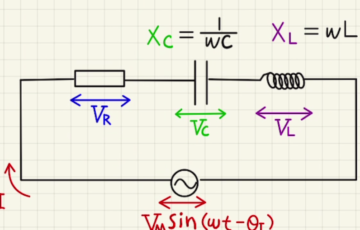
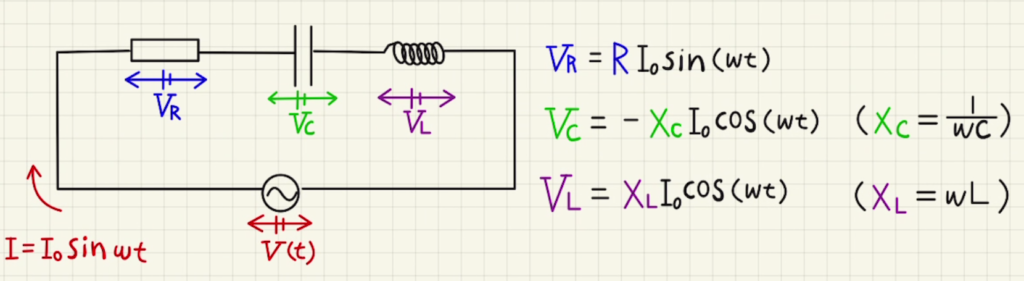
こちらの、RLC直列回路を参考にしていきます。
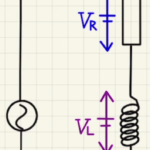
(1)図2から、流れる電流は角振動数 $ω = \frac{2 π}{T}$ とすると
$I = I_{0} \sin ω t$
となることがわかります。
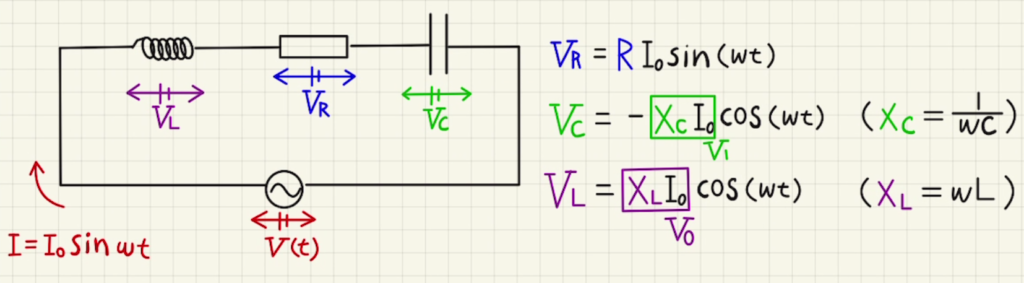
それぞれの電圧は
$V_{R} = R I = I_{0} \sin ω t$
$V_{C} = \frac{Q}{C} = \frac{\int I d t}{C} = - \frac{1}{ω c} I_{0} \cos ω t$
$V_{L} = L \frac{d I}{d t} = ω L I_{0} \cos ω t$
となります。
図2の電圧は $+ \cos$ の形になっていることから、コイル $V_{L}$ とわかりますね。
いわゆる、コイルの電流は(電圧に対して)位相 $\frac{π}{2}$ だけ遅れるというやつです。

まだYとZがわからないので、図3からきめていくことになります。
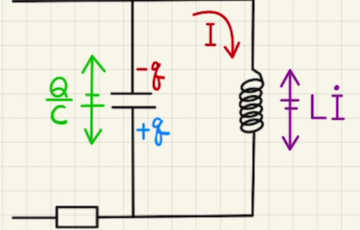
もしYがコンデンサーだとすると、下図のようにスイッチを入れた直後はコンデンサーを素通りし、十分時間が経った後はコイルを素通りしていくため、流れる電流は同じになります。(厳密にはLC並列回路の過渡現象というものですが、高校範囲で扱うことはありません。)

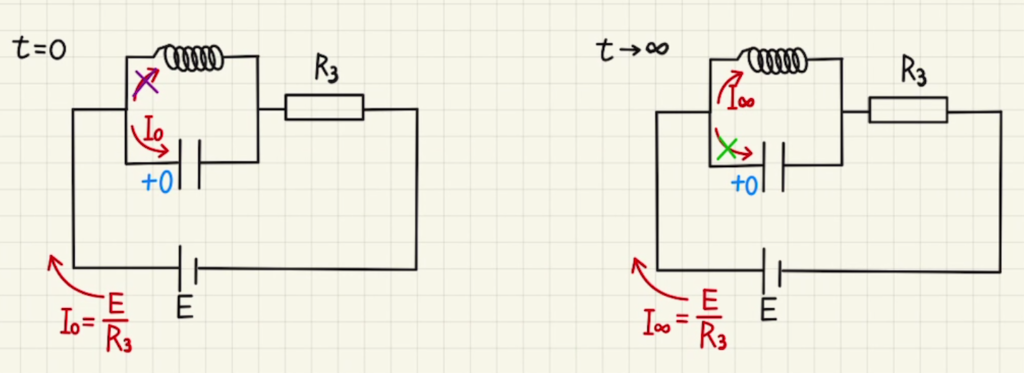
よって、Yは抵抗であると思われますが、実際に見てみましょう。
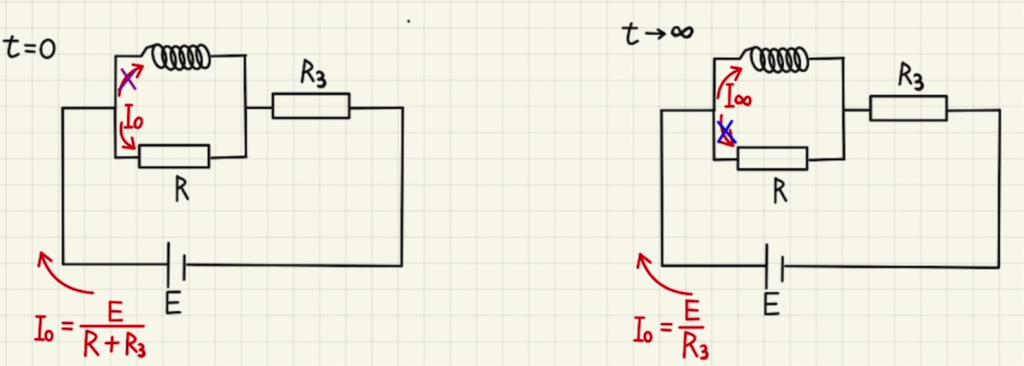
下図のようにスイッチを入れた直後は抵抗にのみし電流が通り、十分時間が経った後はコイルを素通りしていくため、流れる電流は大きくなり条件に合致しそうです。
$20 [Ω]$ の抵抗を $R_{3}$ とすると、左で流れる電流が $I_{0} = \frac{E}{R + R_{3}}$ でこれが2[A]、右で流れる電流が $I_{\infty} = \frac{E}{R_{3}}$ でこれが5[A]となることから、
$R = 30 [Ω]$

以上から、回路を書くと下のようになります。

コイル間の電圧の最大値は
$L ω I_{0} = V_{0}$ より
$L = \frac{V_{0}}{ω I_{0}} = 0.32 [H]$

コンデンサー間の電圧の最大値は
$\frac{1}{ω C} I_{0} = V_{1}$ より
$C = \frac{I_{0}}{ω V_{1}} = 2.5 \times 10^{- 4} [F]$

(2)三つのパーツのうち、電力を消費するのは抵抗だけです。
そのため、 $W = R (\frac{I_{0}}{\sqrt{2}})^{2} = 60 [W]$

(3)コンデンサー間の電圧が0になるのは $\cos ω t = 0$ つまり、 $ω t = \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}$ となります。
よって時刻は $t = \frac{1}{4} T, \frac{3}{4} T, \frac{5}{4} T$ から、 $1.0 \times 10^{- 2}, 3.0 \times 10^{- 2}, 5.0 \times 10^{- 2}$

(4) $t = 1 \times 10^{- 2} = \frac{1}{4} T$ のとき、 $ω t = \frac{π}{2}$ から $\sin ω t = 1, \cos ω t = 0$ なので、
$V = V_{R} + V_{C} + V_{L} = R I_{0} + 0 + 0 = R I_{0} = 60 [V]$

$t = 4 \times 10^{- 2} = T$ のとき、 $ω t = 2 π$ から $\sin ω t = 0, \cos ω t = 1$ なので、
$V = V_{R} + V_{C} + V_{L} = 0 - X_{C} I_{0} + X_{L} I_{0} = 50 [V]$

(5)

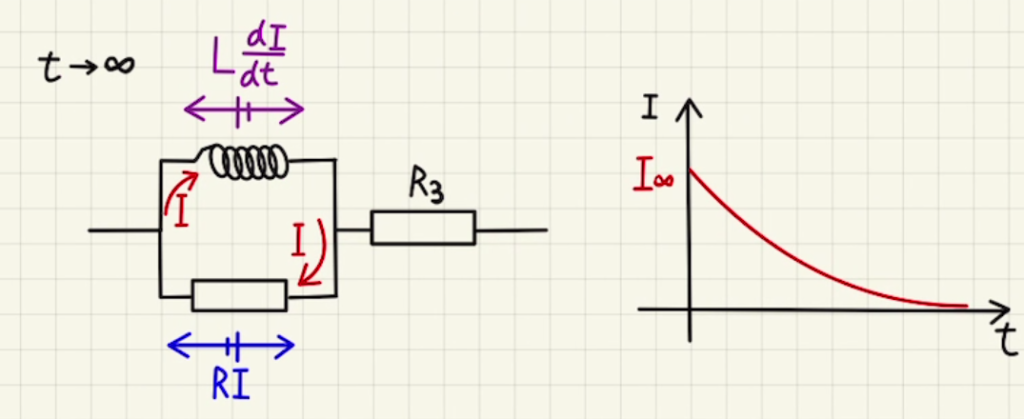
コイルに流れている電流が瞬間的になくなることはないため、スイッチを開いた直後にコイルに流れる電流は $I_{\infty} = \frac{E}{R_{3}}$ となります。
よって抵抗感の電圧差は $R I_{\infty} = 150 [V]$ で、bの方が高くなります。
よって $V_{a} = - 150 [V]$

また、コイルのエネルギーがそのまま抵抗で消費されるため、
$W_{R} = \frac{1}{2} L I_{\infty}^{2} = 4.0 [J]$

補足
並列RL回路の回路の方程式は
$0 = L \frac{d I}{d t} + R I$
よって
$\frac{d I}{d t} = - \frac{R I}{L}$
となるため、この微分方程式を変数分離で解くことができます。

$\frac{d I}{I} = - \frac{R}{L} d t$
を積分して積分定数を $A$ とおくと
$\log I = - \frac{R}{L} + A$
より
$I = e^{A} e^{- \frac{R t}{L}}$
初期値から $e^{A} = I_{\infty}$ とわかるため、
$I = I_{\infty} e^{- \frac{R t}{L}}$
となります。
抵抗での時間当たりの消費電力は
$P = R I^{2} = R I_{\infty}^{2} e^{- \frac{2 R t}{L}}$
なので、
$W = \int_{0}^{\infty} P d t = {[- \frac{1}{2} L I_{\infty}^{2} e^{- \frac{2 R t}{L}}]}_{0}^{\infty} = \frac{1}{2} L I_{\infty}^{2}$
とコイルのエネルギーと一致することが確認できました。