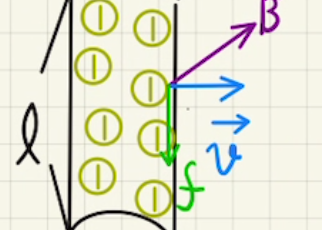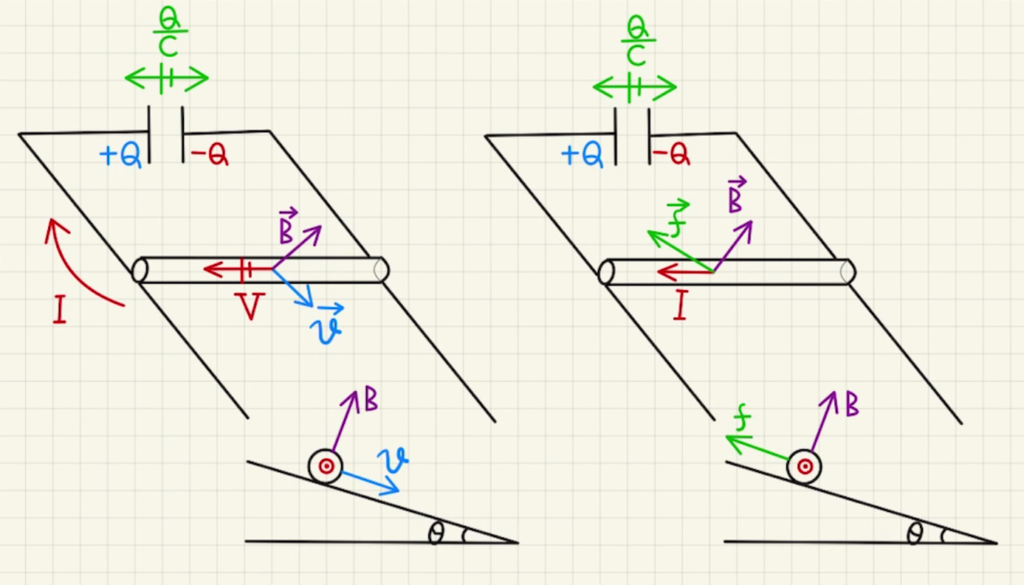
ア $\vec{v}$と$\vec{B}$が垂直なので、誘導起電力は
$V=vBd$
これがコンデンサー間の電圧と一致するため、
$vBd=\frac{Q}{C}$
よって
$$Q=CvBd$$
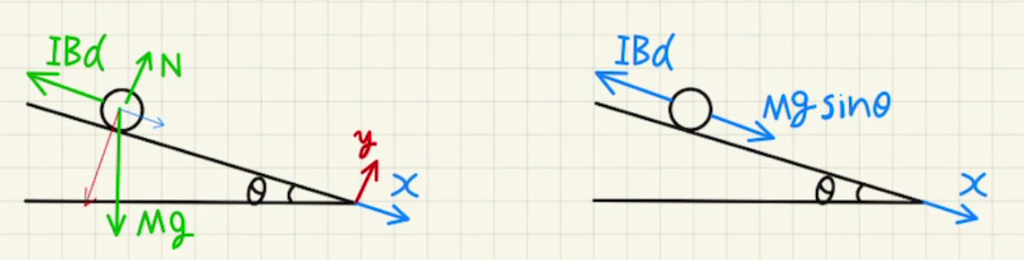
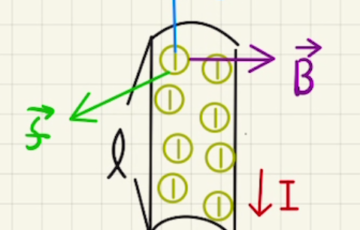
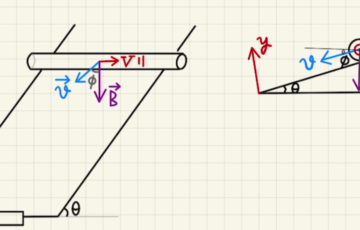
イ ローレンツ力は$\vec{B}$に垂直に働くため斜面上方向($x$マイナス方向)になり、
$x$方向にかかる力は図のようになります。
よって
$$Ma=Mg\sinθ-IBd$$
ウ 流れる電流はそのままコンデンサーに流れ込むため、
$$I=\frac{dQ}{dt}= CBd\frac{dv}{dt} = CBda$$
エ (イ)の結果に(ウ)を代入すると
$Ma=Mg\sinθ- CB^2d^2a$
よって、
$(M+ CB^2d^2 )a=Mg\sinθ$
から、
$$a=\frac{Mg\sinθ}{ M+ CB^2d^2 }$$
また、電流は
$$I=CBda=\frac{CBdMg\sinθ}{ M+ CB^2d^2 }$$
オ 加速度一定より$v=at$となるので、
$x=\frac{1}{2}at^2= \frac{v^2}{2a} $
よって、
$$v=\sqrt{2ax}= \sqrt{ \frac{2Mgx\sinθ}{ M+ CB^2d^2 } } $$
・別解
エネルギー保存則より、
失った位置エネルギー = 運動エネルギー + コンデンサーの静電エネルギー
\begin{align}
Mgx\sinθ &=\frac{1}{2}Mv^2+\frac{Q^2}{2C}\\
&=\frac{1}{2}Mv^2+\frac{(CBd)^2}{2C}v^2\\
&= \frac{1}{2} \left(M+C(Bd)^2\right)v^2\\
\end{align}
よって
$$v= \sqrt{ \frac{2Mgx\sinθ}{ M+ CB^2d^2 } } $$
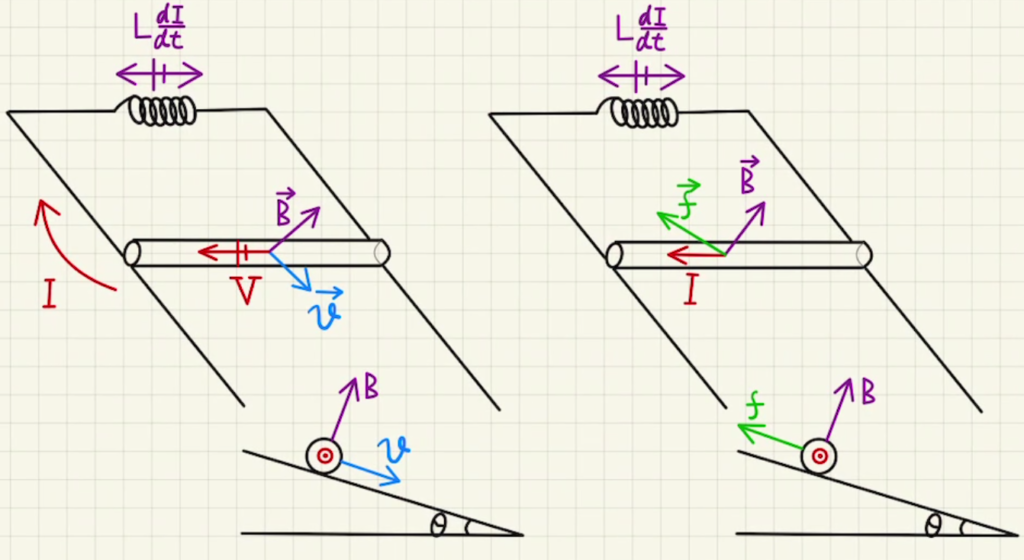
カ Ⅰと同じく、誘導起電力は
$V=vBd$
となります。
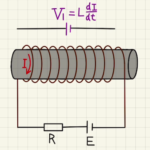
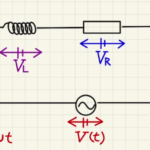
これはコイル間の電圧に一致するため、
$vBd=L\frac{dI}{dt}$
また、$v= \frac{dx}{dt} $から
$Bd\frac{dx}{dt}=L\frac{dI}{dt}$
よって、
$$ dI =\frac{Bd}{L} dx $$
キ
(カ)の式の両辺を積分すると、
$ I =\frac{Bd}{L} x + x_0$
$x_0$は積分定数であり、$I(x=0)=0$より$x_0=0$
よって
$$ I =\frac{Bd}{L} x $$

ク
$x$方向の運動方程式は
$Ma=Mg\sinθ-IBd$
これに(キ)の答えを代入すると
$$Ma=Mg\sinθ-Bd\frac{Bd}{L} x $$
ケ
これより$\ddot{x}=a$は
$$ \ddot{x} =-\frac{ B^2d^2 }{ML} \left(x – \frac{LMg\sinθ}{ B^2d^2 } \right)$$
ここで$ω= \frac{Bd}{\sqrt{ML}} $、$x_c= \frac{LMg\sinθ}{ B^2d^2 } $とすると、
$$ \ddot{x} =-ω^2 (x – x_c)$$
この微分方程式を解くと、単振動の式より、
$$x(t) = (x(0) – x_c ) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt} + x_c $$
となります。
今回、初期値は$ x(0) =0, v(0) = 0$より、
$$x(t) = – x_c \cos{ωt} + x_c ①$$
そのため振幅は、
$$A= x_c = \frac{LMg\sinθ}{ B^2d^2 } $$
コ 周期は
$$T=\frac{2π}{ω}= 2π \frac{\sqrt{ML} }{ Bd } $$
サ
①を微分して
$$v(t) = x_cω \sin{ωt} $$
より
$$\left( \frac{x – x_c }{ x_c } \right)^2 + \left( \frac{v}{ x_cω } \right)^2 = 1$$
となります。
よって
$v= \sqrt{ ω^2 x_c^2 – (ω (x – x_c ))^2 }$
これに$ ω,x_c $を代入すると、
$$v= \sqrt{ 2gx\sinθ – \frac{ B^2d^2}{ LM } x^2}$$