名問の森Ⅱ 43 解説

(1)
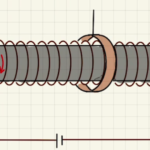
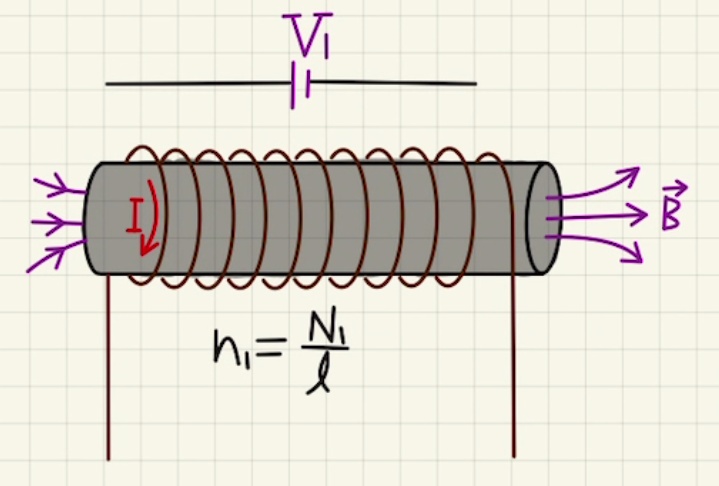
1[m]あたりの巻き数は$n_1=\frac{N_1}{l}$より
$$B=μ_0n_1I= μ_0 \frac{N_1}{l}I$$

(2)微小量$ΔI$は$dI$を書き換えてるにすぎません。(厳密には$ΔI$はただの小さい数で、$dI$は無限小)
磁束$Φ$は
$$Φ=BS= μ_0 \frac{N_1}{l}IS$$
となるため、これによって起こる誘導起電力は
\begin{align}
V_1&=-N_1\frac{dΦ}{dt} \\
&= -μ_0 \frac{N_1^2}{l}S \frac{dI}{dt} \\
&≈ -μ_0 \frac{N_1^2}{l}S \frac {ΔI}{Δt} \\
\end{align}
これは電気が増える方向$ \frac{dI}{dt}$に対して逆向きに、大きさ$ μ_0 \frac{N_1^2}{l}S \frac{ΔI}{Δt} $の起電力が発生することを表しています。

また自己インダクタンスの式
$$ V_1=-L\frac{dI}{dt} $$と照らし合わせると
$$L = μ_0 \frac{N_1^2}{l}S $$

(3)

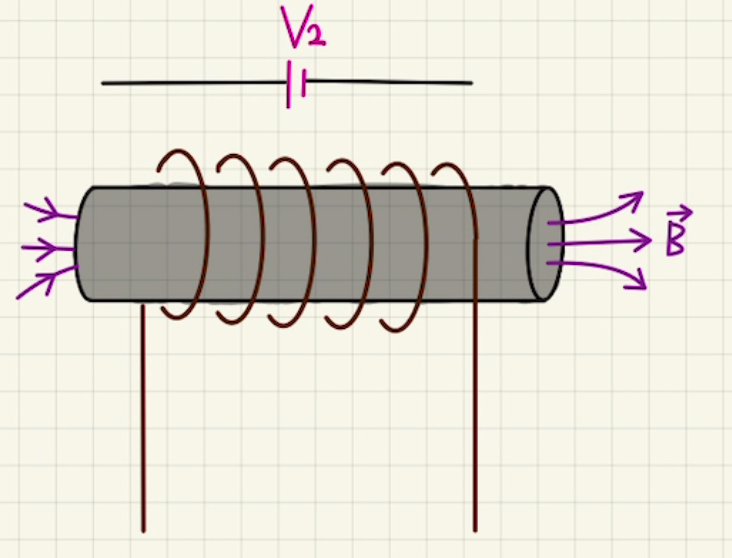
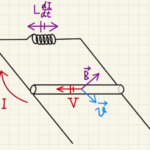
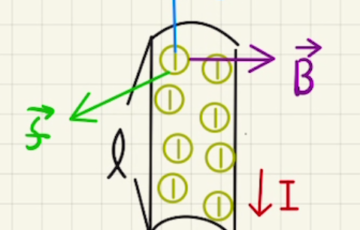
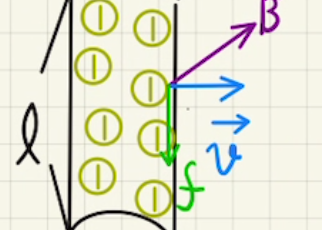
右方向に磁束が増えている場合、左方向に磁場が発生するように電流を流そうと起電力が発生します。
今回ですと図の方向に
\begin{align}
V_2&=-N_2\frac{dΦ}{dt} \\
&= -μ_0 \frac{N_1N_2}{l}S \frac{dI}{dt} \\
&≈ -μ_0 \frac{N_1N_2}{l}S \frac{ΔI}{Δt} \\
\end{align}
つまり、
$$ |V_2| ≈ μ_0 \frac{N_1N_2}{l}S \frac{ΔI}{Δt}$$
が左向き方向に発生します。

これが $ V_2= -M\frac{dI}{dt}$
と一致するため、
$M= μ_0 \frac{N_1N_2}{l}S$

・補足
右方向の磁場を正とすると、電流の向きは常に右ネジ方向を正に取らなければならない。
ただし今回は絶対値で処理しているので、正の向きを考える必要はあまりない。

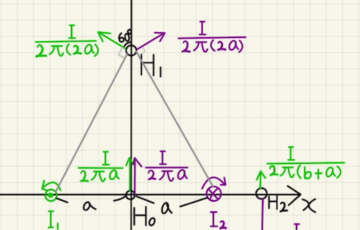
(4)

(ア)

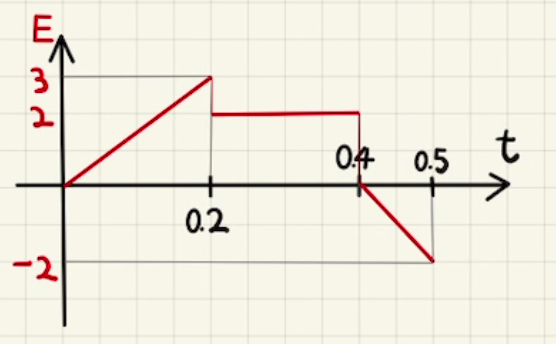
グラフから
$$I =\begin{cases}
&100t & \quad (0≦t≦0.2) \\
&20 & \quad ( 0.2≦t≦0.4 ) \\
&-200t + 100 & \quad ( 0.4≦t≦0.5 )\\
\end{cases}$$
より、これによる誘導起電力は$V_P=L\frac{dI}{dt}$なので
$$V_P =\begin{cases}
&100L & \quad (0≦t≦0.2) \\
&0 & \quad ( 0.2≦t≦0.4 ) \\
&-200L & \quad ( 0.4≦t≦0.5 )\\
\end{cases}$$
$L=10×10^{-3}$より、これを図示すると

(イ)
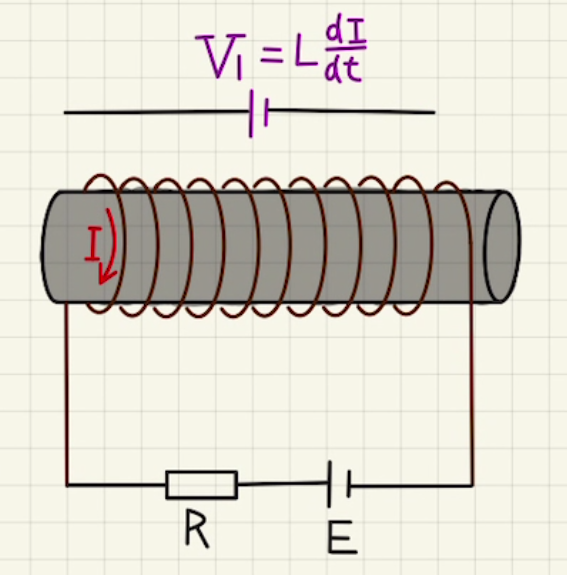
回路の方程式から
$$ E=RI+ L\frac{dI}{dt} $$
となるため、
$$E =\begin{cases}
& 100Rt +100L& \quad (0≦t≦0.2) \\
&20R & \quad ( 0.2≦t≦0.4 ) \\
&(-200t + 100)R-200L & \quad ( 0.4≦t≦0.5 )\\
\end{cases}$$
これに $L=10×10^{-3}$および$R=0.1$を代入すると
$$E =\begin{cases}
& 10t+1 & \quad (0≦t≦0.2) \\
&2 & \quad ( 0.2≦t≦0.4 ) \\
&-20t + 8 & \quad ( 0.4≦t≦0.5 )\\
\end{cases}$$
これを図示すると、