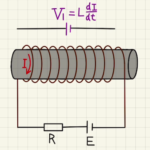
Ⅰ 問題文には書いていませんが、自己インダクタンスは無視できるようです。そうでないと時刻によって流れる電流が変わってしまいます。
恐らく十分に電流が安定した後を想定しているのでしょう。(本来はそれも問題文にかくべきですが…)
そのため、回路としてはコイルを抵抗として扱えばよさそうですね。
コイルの抵抗値は長さに比例するので、長さ$l$当たりの抵抗を$R$としましょう。
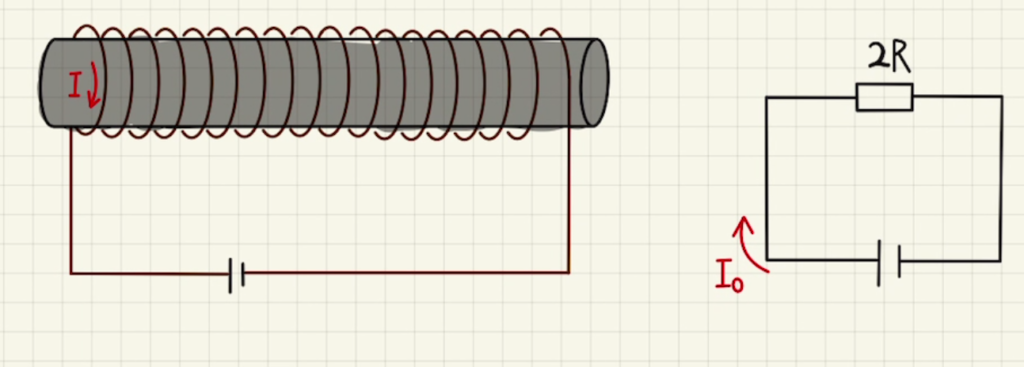
$V_0=RI_0$
より $I_0=\frac{V_0}{2R}$
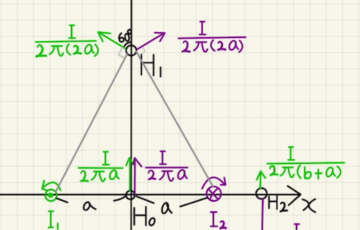
コイル内部に発生する磁場は
$H_0=nI_0= n\frac{V_0}{2R} $
(1)
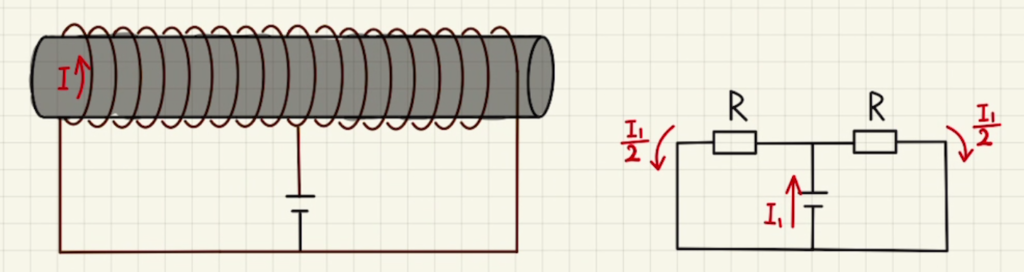
この場合か流れる電流を$I_1$とすると、コイルに流れる電流は$\frac{I_1}{2}$なので
$V_0=R \frac{I_1}{2} $
よって$ I_1 = \frac{2V_0}{R}=4I_0 $
コイル内部で逆向きにそれぞれ磁場を発生させるため、打ち消しあい、
$H_0=0$
(2)
コイルに使われている導線自体は長さが変わらないので抵抗値は変わりません。
よって回路は問題文のものと変わらず$I_2=I_0$
1m当たりの巻き数は半分なるので磁場は$H_2=\frac{1}{2}H_0$
(3)
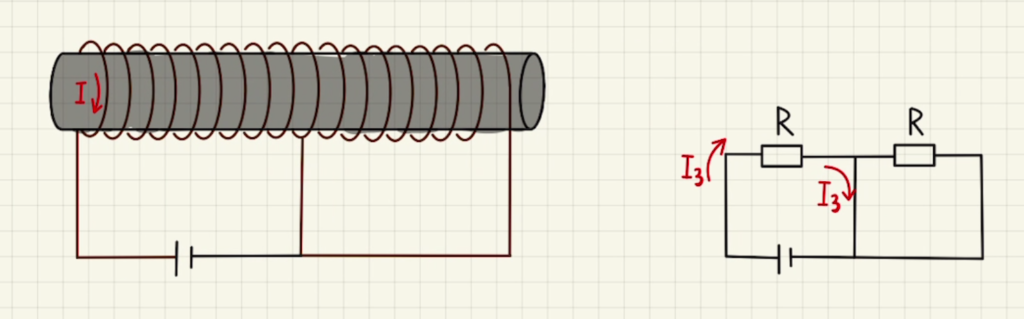
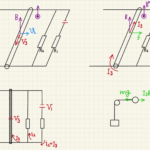
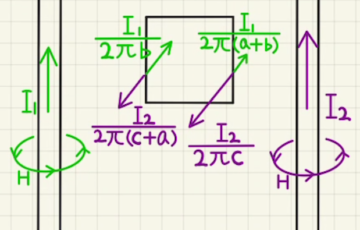
図のような回路で流れるため、
$V_0=RI_3$
より、$I_3=\frac{V_0}{R}=2I_0$
このときコイル内部(中央付近)には二倍の磁場$H_3=2H_0$が発生します。
今回はBはコイルの端となるため、その半分の$H’_3=H_0$となります。
・補足
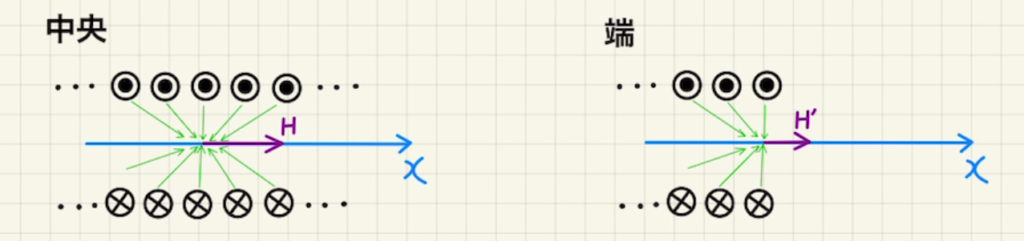
なぜコイルの端では磁場が中央付近の半分になるのかはビオサバールの法則で説明がつきます。
コイルの中央付近では、左右どちらの電流からも影響を受けるのに対し、端では片側の電流の影響しか受けません。
そのため、半分の磁場しか発生しなくなります。
Ⅱ
ここからの問題は数値で計算するよりも、より定性的な説明の問題となります。
とりわけ、コイルの端付近では磁場が複雑になっているため、計算するのは困難でしょうから、だいたい磁場がどうなっているかを考えられれば十分です。
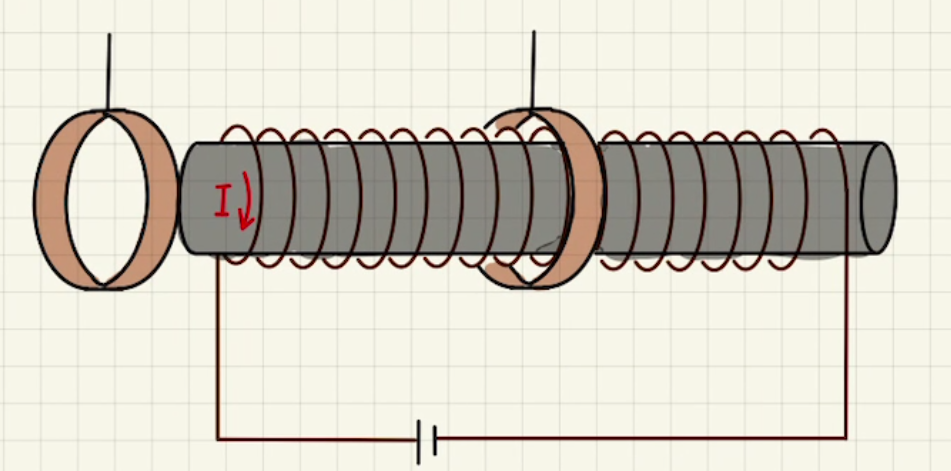
(4)
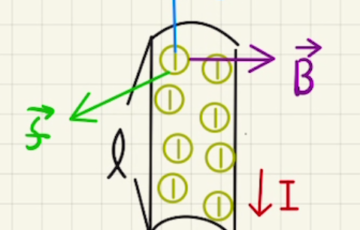
コイルが図の方向に電流が増えていくため、それに伴いコイル内部も右方向に磁場が増え、磁束も増加します。
そのため、それを打ち消す形で電流を流そうという誘導起電力が発生します。
よって流れる電流はコイルの電流と逆向きとなります。
(5)
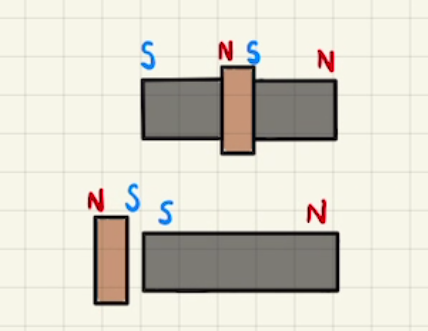
今回の問題に関しては、コイルは磁石のようになり流れる方向の右ネジ向きにN極になる、程度の理解でいいでしょう。
図から、$R_1$には斥力が働き左に動くが、$R_2$は対称性から引力が釣り合うため力が働きません。
別解のように磁場の分布からローレンツ力として考える見方もあります。
・別解
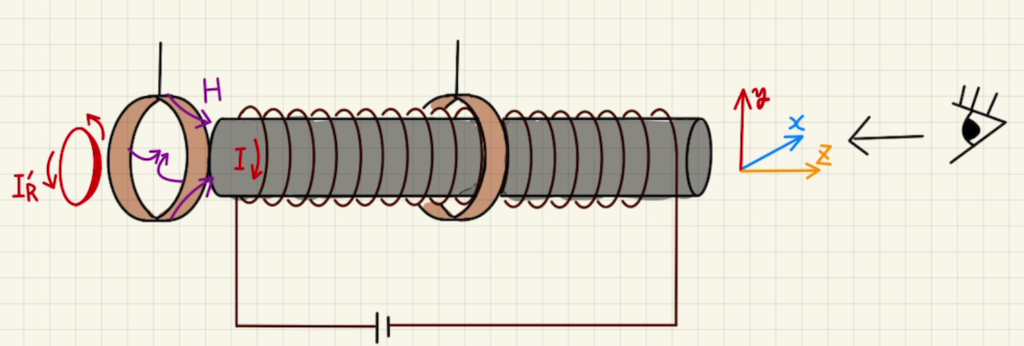
コイルの巻いてある外側には磁場は発生せず、$R_2$の電流が流れている部分には磁場がないといえます。そのため、 $R_2$にはローレンツ力は働きません。
考えるべきは $R_1$でしょう。
コイルの左端より少し左側では磁場がコイル中央に向かう形で発生しています。ちょうど掃除機で空気を吸引しているようなイメージです。
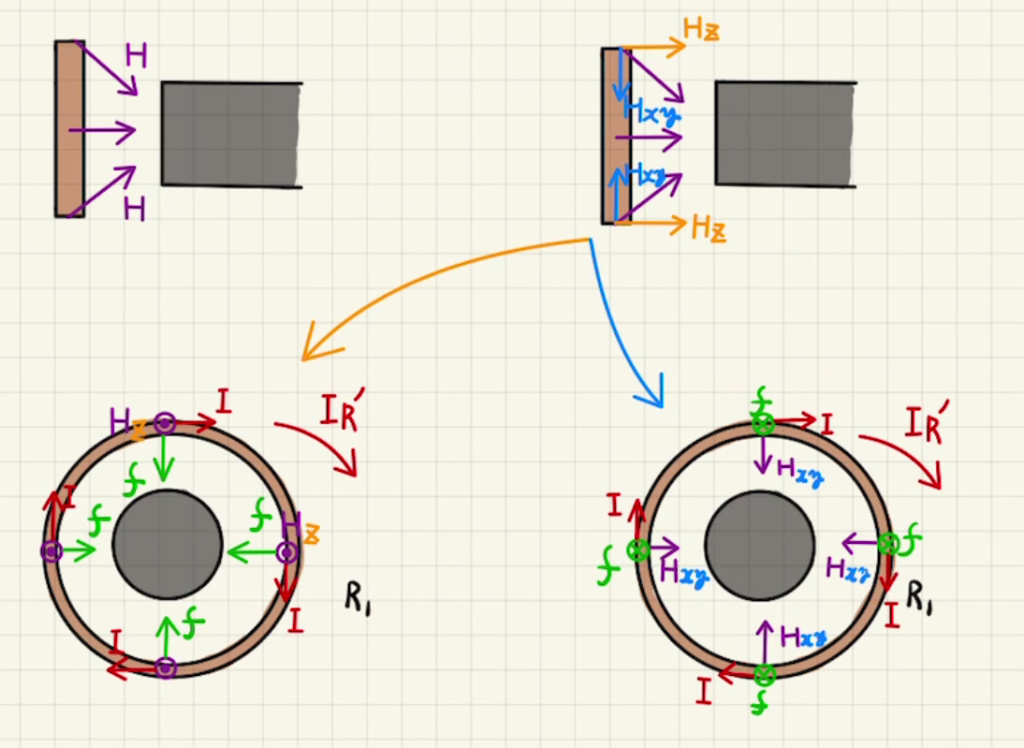
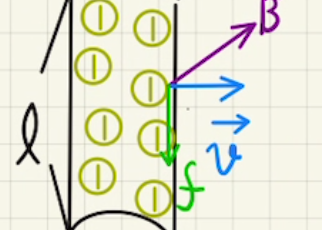
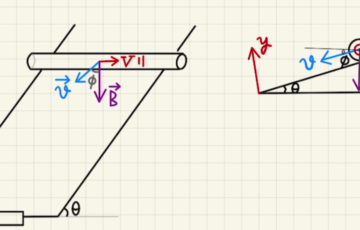
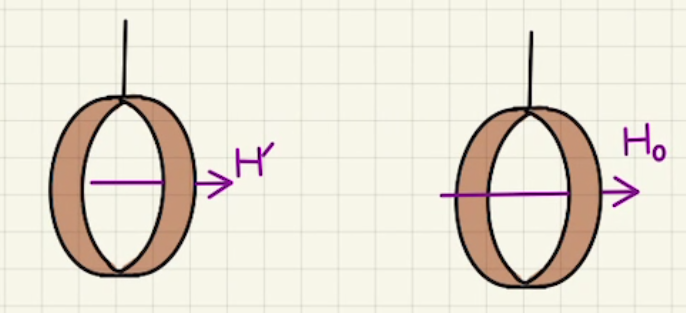
このとき、$yz$平面で見ると、下図のように磁場が発生しており、コイル平行方向の磁場$H_z$と、それ以外の$xy$平面成分の磁場$H_{xy}$に分解することができます。
それぞれの部分(長さ$Δl$と置く)に対してかかるローレンツ力は
$$f=\vec{I}×\vec{B}Δl= μ\vec{I}×\vec{H}Δl ∝ \vec{I}×\vec{H}$$
となるため、$\vec{I}×\vec{H}$の右ネジの方向となります。
磁場$H_z$が引き起こすローレンツ力を見ると、左下の図のように円の中心方向に向かって力が働きます。
この力は上下左右でつり合っているため、合力は$0$となります
磁場$H_{xy}$が引き起こすローレンツ力は右下のようになっており、全ての場所で紙面奥方向($z$マイナス方向) となります。
これがコイルに対する斥力の正体です。