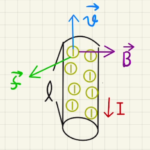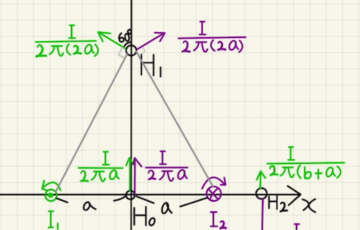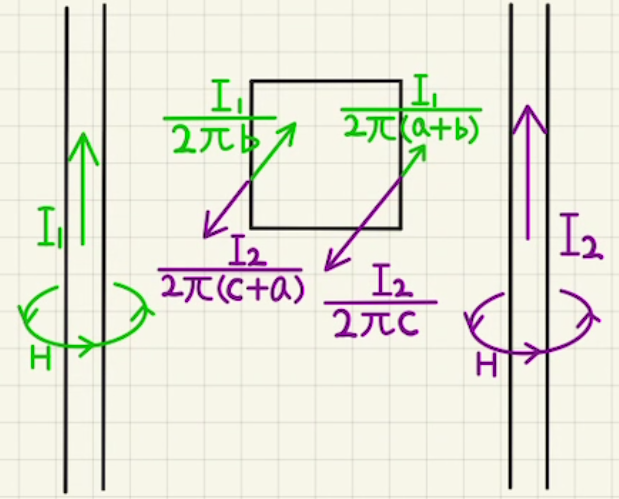
(1)緑の電流は右ネジ方向に磁場を発生させ、ADでは$\frac{I_1}{2πb}$の磁場が発生します。
(2)$I_2$も文字ネジ方向に磁場を発生させるため、上方向に流れるとADで逆方向に磁場が発生します。
(3)紫の電流がADに作る磁場は $\frac{I_2}{2π(a+b)}$なので
$\frac{I_1}{2πb} =\frac{I_2}{2π(c+a)} $となればよく、
$I_2= \frac{ c+a }{b} $
(4)BDでの磁場の大きさは
$H_{BC}= \frac{I_2}{2πc}- \frac{I_2}{2π(a+b)} $
よって
$H_{BC}= \frac{1}{2π}\frac{a(a+b+c)}{bc(a+b)} $
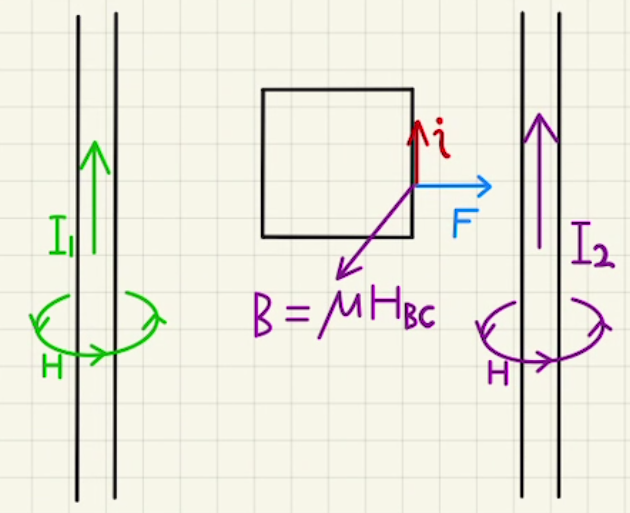
(5)(6) BCでの磁束密度は$\vec{B}=μ\vec{H_{BC}}$
BCで発生するローレンツ力は
$\vec{F}=\vec{i}×\vec{B}l$
$\vec{i}$と$\vec{B}$は垂直であるため、 ローレンツ力の大きさは
$\vec{F}=iBl$
となり、向きは$\vec{i}$と$\vec{B}$が作る右ネジの向き、すなわち右方向となります。
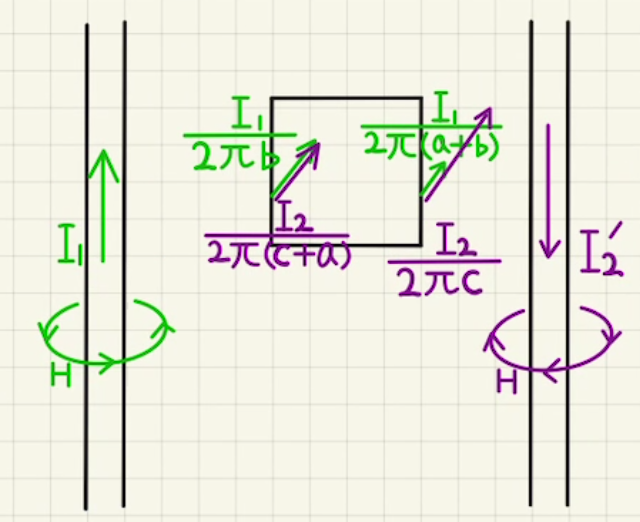
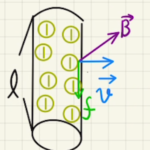
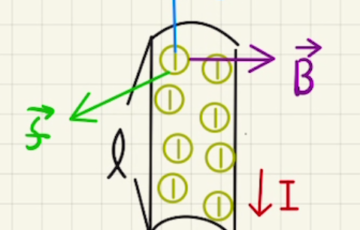
(7)紫の電流を逆向きに流す図のように磁場が発生します。
BCに発生する磁場の大きさを$H’_{BC}$、 ADに発生する磁場を$H’_{AD}$とすると、それぞれに発生するローレンツ力の大きさは
$ F_{BC} =iμH’_{BC}l$
$ F_{AD} =iμH’_{AD}l$
となる。
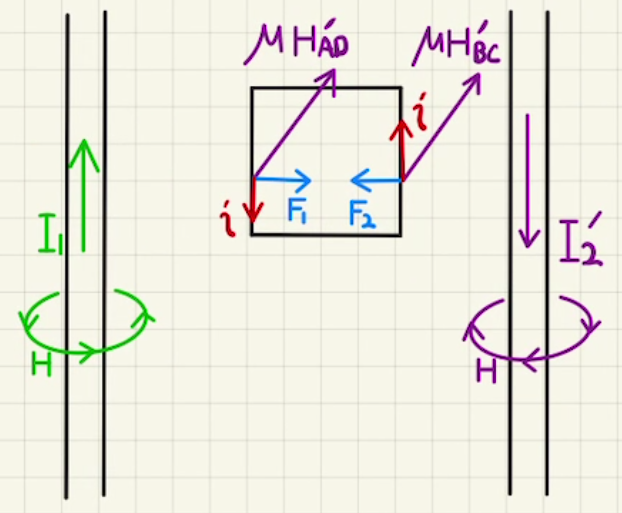
そのため、この二つの力が釣り合う条件は
$ H’_{BC} = H’_{AD}$
つまり
$ \frac{I_1}{2πb}+ \frac{I_2′}{2π(c+a)} = \frac{I_1}{2π(a+b)}+ \frac{I_2′}{2πc} $
よって、
$ I_2′ =\frac{c(a+c)}{b(a+b)}I_1$