解答欄

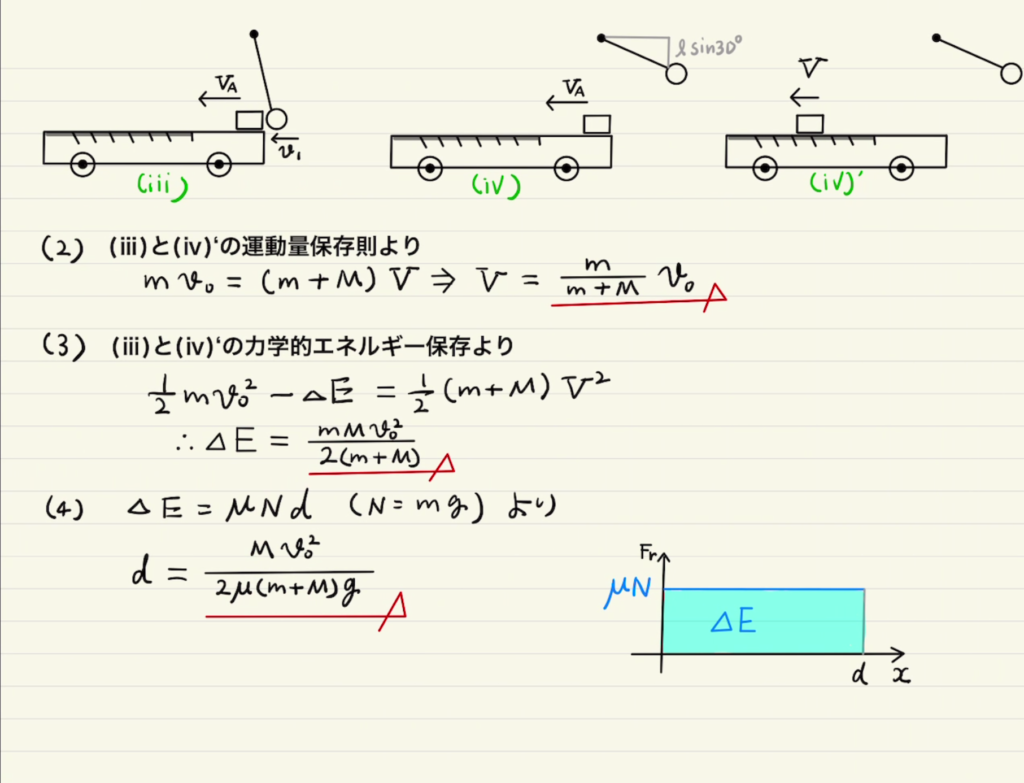
今回も固定されていない台ということで運動量保存則が使えそうです。
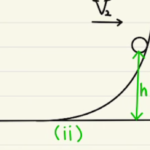
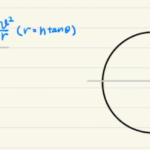
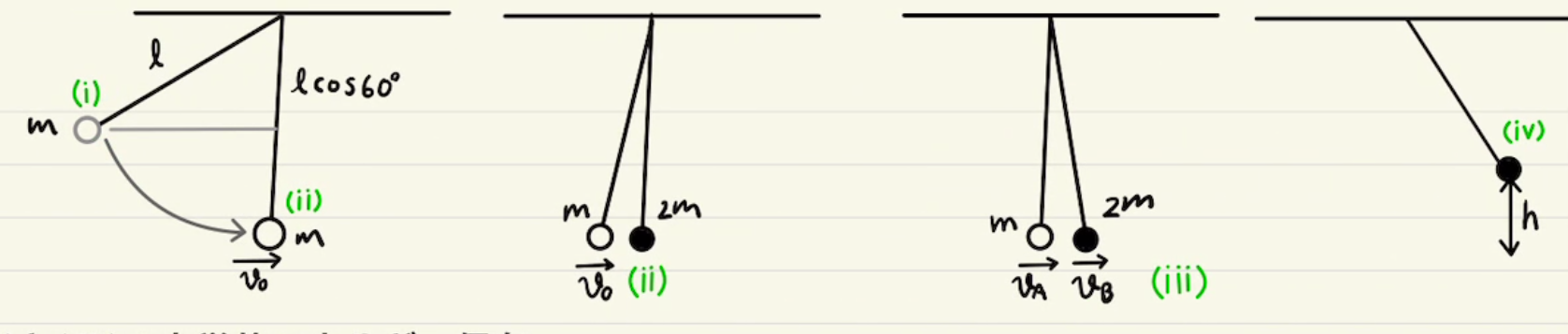
まずは紐が振り子となるように落とすため、運動エネルギー保存を使います。
衝突で運動量保存し、その後振り子は力学的エネルギーを保存しながら上に戻ります。
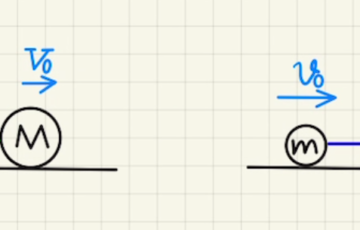
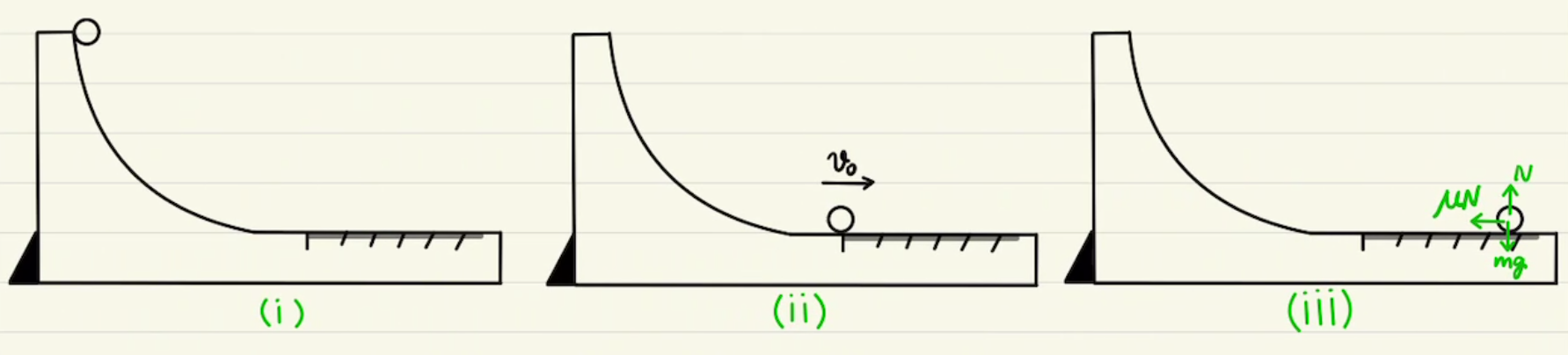
押し出された物体は運動量が保存します。力学的エネルギーは摩擦によって一部消失します。
(4)は問19を保存量ベースで解きなおしたものと言えそうです。
補足
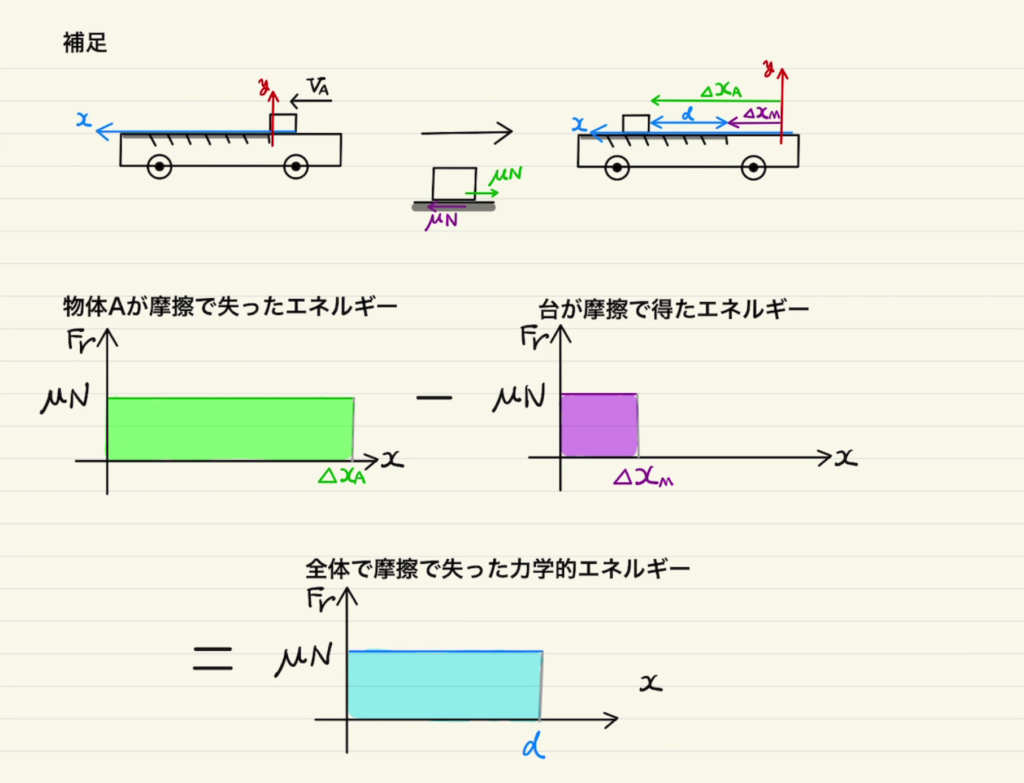
(3)(4)の問題分には二物体の系のエネルギー損失について問われています。
答えでは$”摩擦力”×”物体が相対的に動いた距離”$となっています。
なぜそうなるのか、少し見てみます。
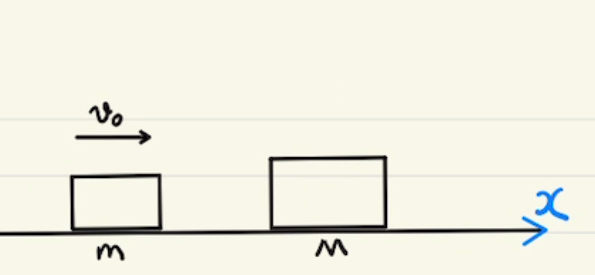
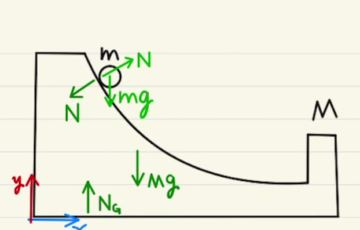
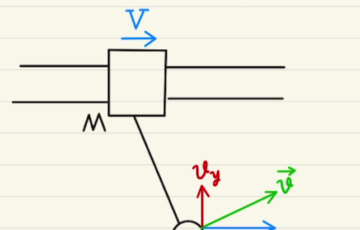
物体Aは$x$負の方向に摩擦力がかかりながら$x$プラス方向に動くため、摩擦力によってエネルギーは失われます。
動いた距離が$Δx_A$なら$μN Δx_A$ですね。
一方台は $x$正の方向に摩擦力がかかりながら$x$プラス方向に動くため、摩擦力によってエネルギーは 増えます。
動いた距離が$Δx_M$なら$μNΔx_M$ですね。
これらの差分をみると全体で失ったエネルギーが見れます。
計算してみると$μNd$ となり、$摩擦力×Aが相対的に動いた距離$ に相当することがわかりました。
こういった問題では具体的な説明なく相対位置と絶対位置を混同して解説していることが多いですが、あいまいになった場合は絶対座標でどうなっているのかを一旦確認するのをおすすめします。