電磁気学⑤ 交流　

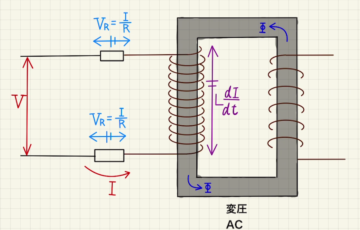
いままでの電流の問題では、基本的に起電力は変化しないものとして扱ってきました。
しかし、日常のなかで使われている電流は電圧が変化しているものの方が多いです。

今回は主に$\sin$の形をした電圧をかけた時を考えます。
電流や電圧が「$A\sin{(〇〇)}$」の形になったときに、Aを振幅、$\sin$の中身の$〇〇$を位相と言います
振幅や位相に注目しながら回路の電流や電位の変化を見ていきましょう。

抵抗とコンデンサーとコイル

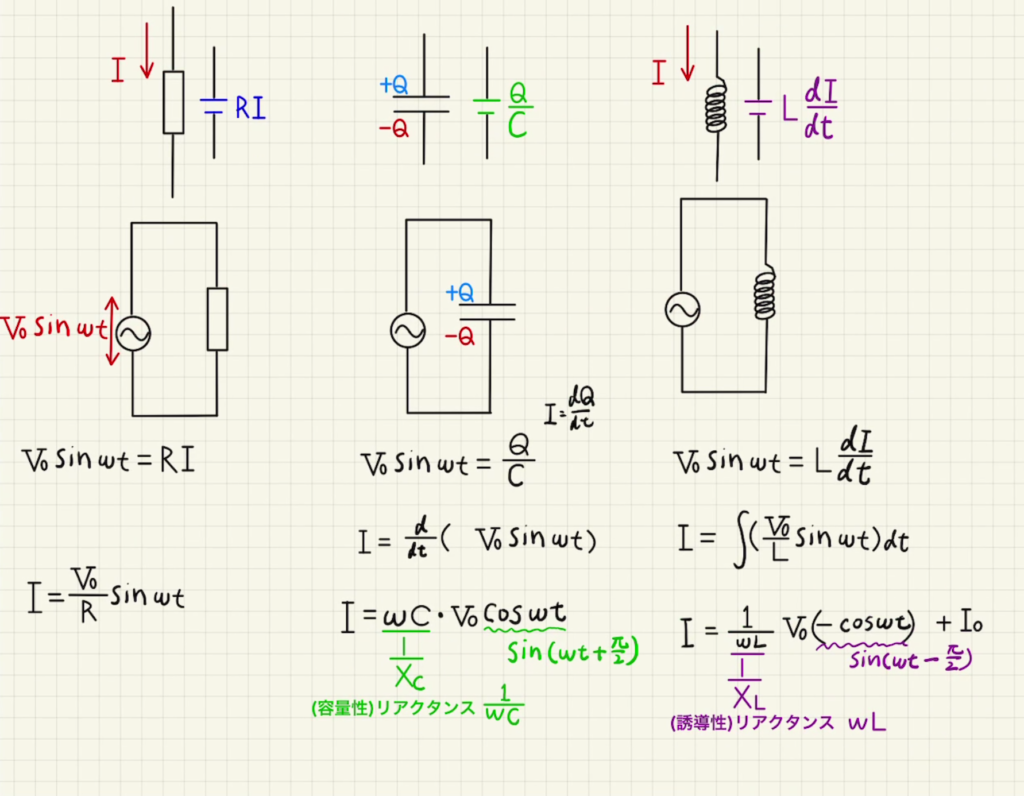
電圧$V=V_0\sin{ωt}$で時間変化するというように書けます。
交流における三つのパーツについて一つずつ考えていきましょう。

・抵抗
抵抗に電流$I$が流れるとその逆方向に$RI$の電位差が生まれます。
これが $V_0\sin{ωt}$と合致するため、回路方程式は
$V_0\sin{ωt}＝RI$
から
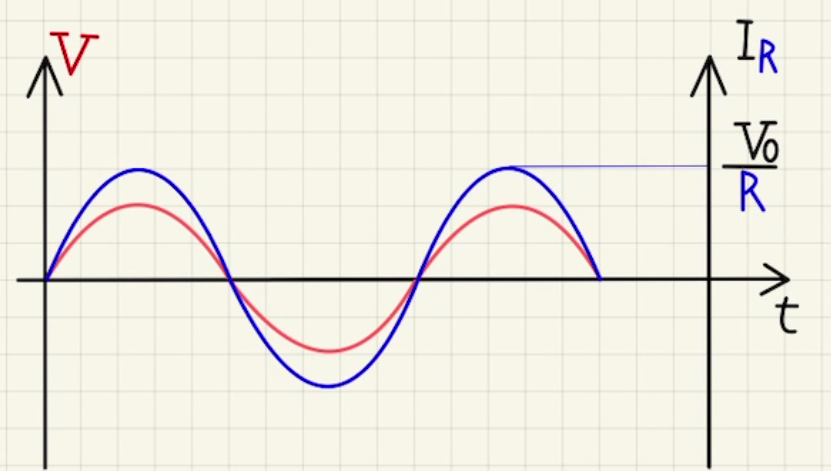
$$I=\frac{V_0}{ {\color{blue} R} }\sin{ωt}$$
となり、電流は電圧と同じ$\sin$の形となります。

・コンデンサー
コンデンサー間の電圧は正に帯電した方向に$V_C=\frac{Q}{C}$となります。
そのため、回路の方程式は
$V_0\sin{ωt}= \frac{Q}{C}$
となるため、
$ Q = CV_0\sin{ωt}　…①$
となります。
また、コンデンサーから出入りする1秒あたりの電荷が電流となるため、
$I=\frac{dQ}{dt}$となります。
①の式の両辺を微分すると$$ I= ω CV_0 \cos{ωt}$$となることがわかりました。

抵抗と同じように、
$ I= \frac{V_0}{〇〇}\sin{(ωt + 〇〇)} $
と書き換えたいと思います。
ここで$ {\color{green} X_C=\frac{1}{ ω C } } $とおくと、
$$I= \frac{V_0}{ {\color{green} X_C} } \sin{(ωt + \frac{π}{2})}$$
と書き換えることができました。
このとき $X_C =\frac{1}{ ωC }$は容量性インダクタンスといい、コンデンサーにおける抵抗値に相当します。
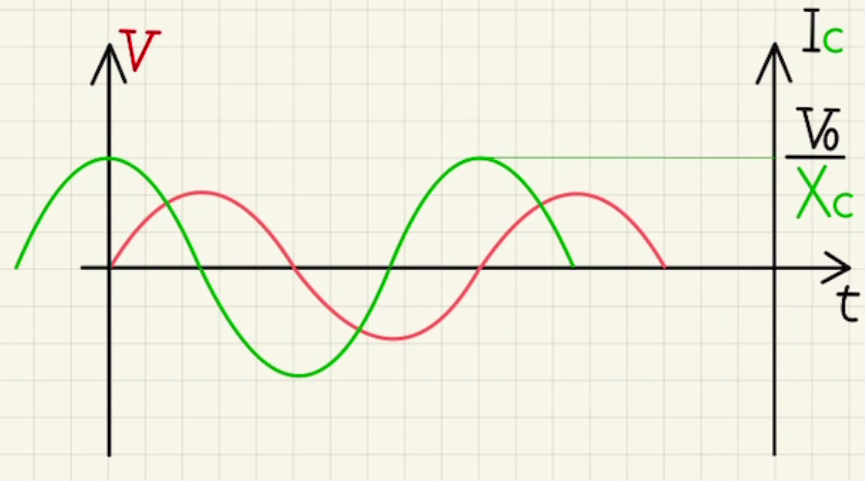
また、電流は電圧に比べて位相$ \frac{π}{2}$進んでいるような波形になります。

・コイル
コイルの間の電圧は電流が増える方とは逆向きに$V_L=L\frac{dI}{dt}$となります。
そのため、回路の方程式は
$V_0\sin{ωt}= L\frac{dI}{dt} $
となるため、
$ \frac{dI}{dt} = \frac{V_0}{L}\sin{ωt}$
となります。
これの両辺を積分をすると、
$I = -\frac{V_0}{ ωL}\cos{ωt}＋I_0$
となります。$I_0$は積分定数であり、初期電流に相当しますが、通常は$0$となるため、下の式となります。
$$I = -\frac{V_0}{ ωL}\cos{ωt}$$
これもまた抵抗と同じように、
$ I= \frac{V_0}{〇〇}\sin{(ωt + 〇〇)} $
と書き換えたいと思います。
ここで$ {\color{purple} X_L= ωL }$とおくと、
$$I= \frac{V_0}{ {\color{purple} X_L} } \sin{(ωt – \frac{π}{2})}$$
と書き換えることができました。
このとき $X_L=Lω $は誘導性インダクタンスといい、コイルにおける抵抗値に相当します。
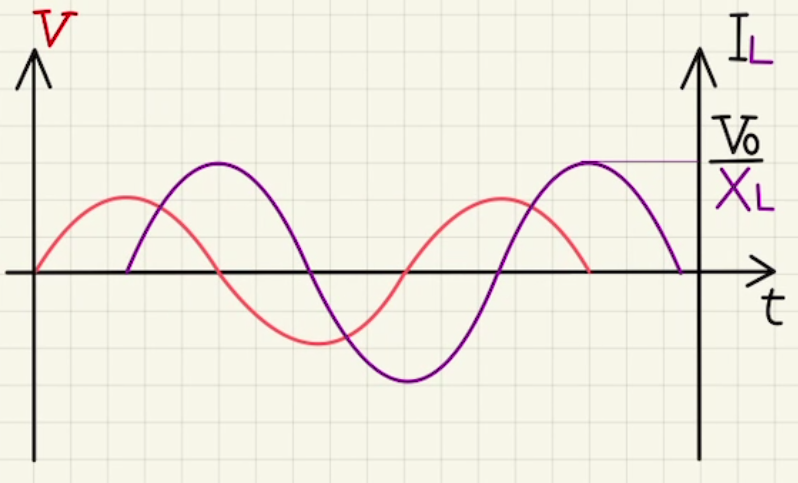
また、電流は電圧に 比べて位相$ \frac{π}{2}$遅れているような波形になります。

実効値

交流では電圧が時間変化するため、直流に換算すると実質的にどれくらいの電圧のもの電池と同じようなものなのか定めます。
ここで定義と基準となるのが抵抗での消費電力です。

交流では電圧が時間変化するため、直流に換算すると実質的にどれくらいの電圧のもの電池と同じようなものなのか定めます。
ここで定義の基準となるのが抵抗での消費電力です。

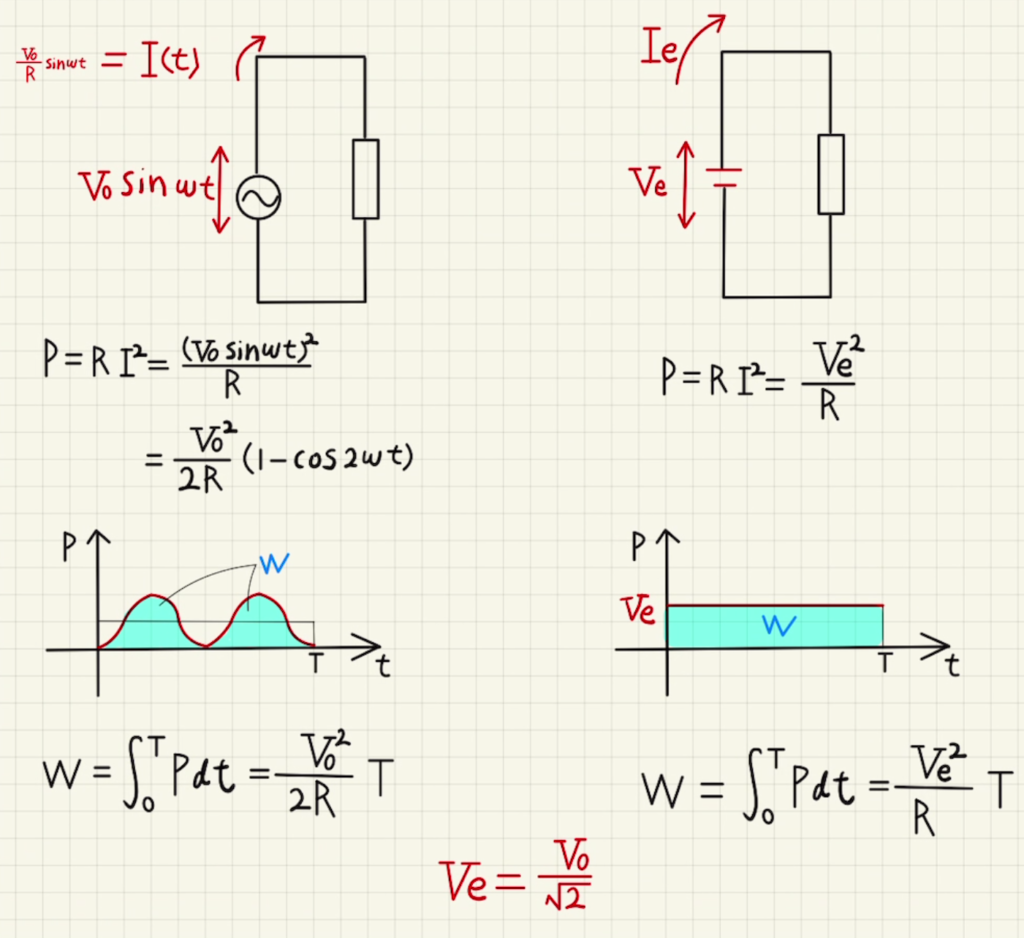
抵抗値$R$の抵抗に電圧$V_0\sin{ωt}$をかけたとき、1秒あたりの消費電力は
$$P= \frac{V^2}{R} =\frac{ (V_0\sin{ωt})^2 }{R}$$
となります。

よって1周期経つまでに抵抗で消費したエネルギーは、

\begin{align}
\int_0^TPdt&=\int_0^T \left( \frac{ (V_0\sin{ωt})^2 }{R} \right)dt \\
&= \frac{V_0^2}{2R} \int_0^T ( 1-\cos{2ωt} )dt \\
&= \frac{V_0^2}{2R} \left[ t-\frac{1}{2ω}\cos{2ωt} \right]_0^T \\
&=\frac{V_0^2}{2R}T \\
\end{align}
となります。
この値が直流の消費電力$$ W = \frac{V_e^2}{R}T $$と等しくなると考えます。

よって電圧の実効値は$$ V_e = \frac {V_0}{\sqrt{2}}$$と求めることができました。



電流の場合も同様に、電流$I=I_0\sin{ωt}$が流れているときの1秒あたりの消費電力は
$$P= RI^2=R(I_0\sin{ωt})^2　⇒　\int_0^TPdt= \frac{1}{2}RI_0^2T$$
となるため、$$ I_e = \frac {I_0}{\sqrt{2}}$$と求められます。

以上のことから1秒当たりの平均消費電力は
$$\bar{P}= RI_e^2=\frac{V_e^2}{R}=V_eI_e$$

並列RLC回路

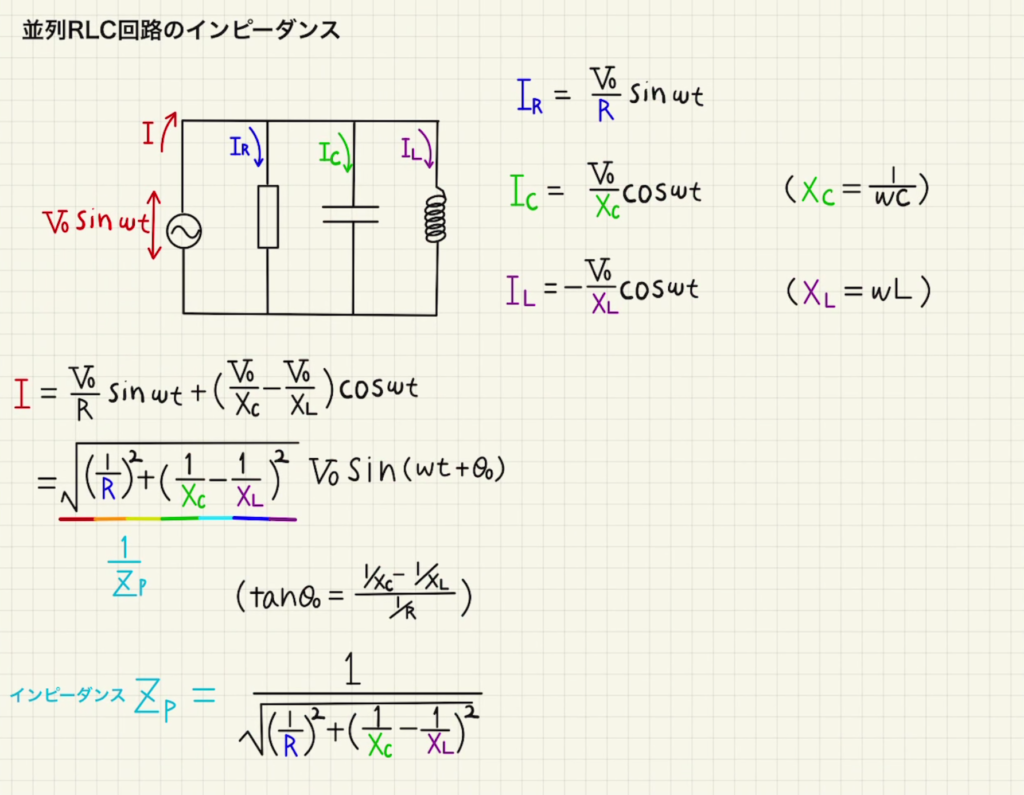
抵抗とコンデンサーとコイルの三つを並列に並べて電圧$V_0\sin{ωt}$をかけたときに、流れる電流と各パーツの電圧を考えます。

各パーツには電圧$V_0\sin{ωt}$と同じだけの電位差が発生します。
「抵抗とコンデンサーとコイル」 の項目でやったようにそれぞれのパーツに流れる電流は
$$I_R=\frac{V_0}{ {\color{blue} R} }\sin{ωt}$$
$$I_C= \frac{V_0}{ {\color{green} X_C} } \cos{ωt}$$
$$I_L= -\frac{V_0}{ {\color{purple} X_L} } \cos{ωt}$$
となります。

これらの電流を足し合わせた電流が電源から流れる電流と等しくなります。
つまり、
$$I = I_R + I_C + I_L = \frac{V_0}{ {\color{blue} R} }\sin{ωt} + (\frac{V_0}{ {\color{green} X_C} } – \frac{V_0}{ {\color{purple} X_L} }) \cos{ωt} $$
ここで三角関数の合成$a\sin{θ}+ b\cos{θ}=\sqrt{a^2+b^2} \sin{(θ+α)}$(ただし、 $\tan{α}=\frac{b}{a}$ )を当てはめると、
$$I = \sqrt{ \Bigl( \frac{1}{ {\color{blue} R} } \Bigr) ^2 + \Bigl( \frac{1}{ {\color{green} X_C} } – \frac{1}{ {\color{purple} X_L} } \Bigr) ^2} V_0 \sin{(ωt + θ_0)} $$
となります。
ここで、 リアクタンスと同じように
$$ {\color{#20b2aa} Z_p} =\frac{1}{ \sqrt{ \Bigl( \frac{1}{ {\color{blue} R} } \Bigr) ^2 + \Bigl( \frac{1}{ {\color{green} X_C} } – \frac{1}{ {\color{purple} X_L} } \Bigr) ^2} }$$
とおくと、
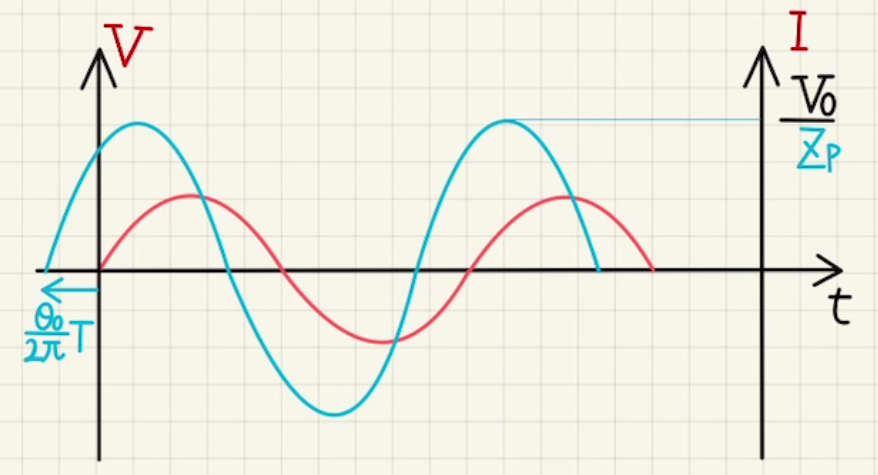
$$I= \frac{1}{ {\color{#20b2aa} Z_p} }V_0 \sin{(ωt+θ_0)}$$
と表せます。 $Z_p$は交流回路における抵抗値に相当し、インピーダンスと言います。

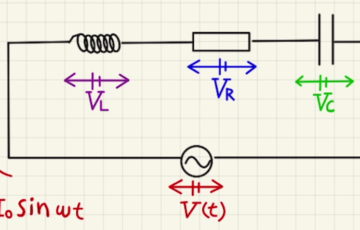
直列RLC回路

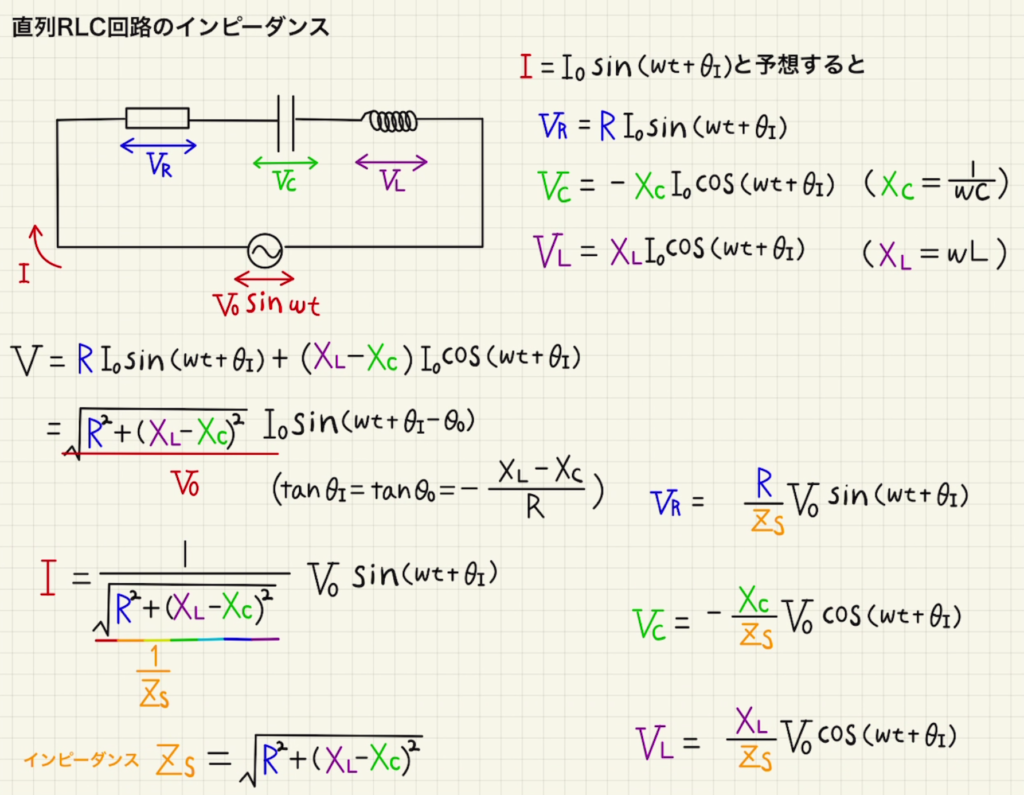
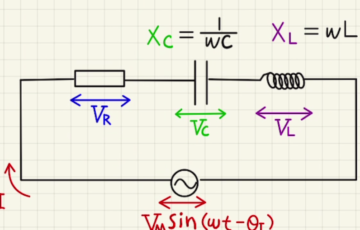
抵抗とコンデンサーとコイルの三つを直列に並べて電圧$V_0\sin{ωt}$をかけたときに、流れる電流と各パーツの電圧を考えます。

今回は完全に0から証明すると大変なので、電流も三角関数の形になるだろうと予測して、計算を進めます。
すなわち$I=I_0\sin{(ωt+θ_I)}$の形であると予測して、 $I_0$と$θ_I$を求めていきます。

・抵抗
抵抗での電位差は$V=RI$から
$$V_R= {\color{blue} R} I_0\sin{(ωt+θ_I)} $$

・ コンデンサー
コンデンサー間の電圧は$V=\frac{Q}{C}$となります。
流れ込んだ電流の蓄積が貯められた電荷であることから、$Q=\int{Idt}$ ($I=\frac{dQ}{dt}$の逆)となり、
$V_C= \frac{1}{C} \int{( I_0\sin{(ωt+θ_I)} )dt} = – \frac{I_0}{Cω} \cos{(ωt+θ_I)} ＋V_0 $
$V_0$は積分定数であり初期電位差に相当しますが、通常はこれは0となります。
これに容量性リアクタンス$X_C=\frac{1}{Cω}$を代入すると
$$V_C= – {\color{green} X_C} I_0 \cos{(ωt+θ_I)} $$

・ コイル
コイル間の電圧は$V=L\frac{dI}{dt}$となります。
これに $I=I_0\sin{(ωt+θ_I)}$ を代入すると
$V_L= Lω \frac{d}{dt} ( I_0\sin{(ωt+θ_I)} ) = Lω \cos{(ωt+θ_I)} $
さらに誘導性リアクタンス $ X_L=Lω $を代入すると
$$V_L= {\color{purple} X_L} I_0 \cos{(ωt+θ_I)} $$

これら三つの電圧を足し合わせると、 $V=V_0\sin{ωt}$と常に一致しなければなりません。
すなわち、
$$V= V_R + V_C + V_L = RI_0\sin{(ωt+θ_I)} + (X_L-X_C)I_0 \cos{(ωt+θ_I)} $$
ここで三角関数の合成$a\sin{θ}+ b\cos{θ}=\sqrt{a^2+b^2} sin{θ+α}$を当てはめると、
$$V=　\sqrt{R^2+ (X_L-X_C)^2 }I_0\sin{(ωt+θ_I-θ_0)} $$
ただし、$tan{ θ_0 }=-\frac{ X_L-X_C }{R}$
この値が常に(どんな$t$でも)等しくなるため、
$V_0 = \sqrt{R^2+ (X_L-X_C)^2 }I_0 $、$ θ_I-θ_0 =0$
このことから、$I_0 = \frac{1}{\sqrt{R^2+ (X_L-X_C)^2 }}V_0 $、 $\tan{θ_I}=-\frac{ X_L-X_C }{R}$

これらの結果から、流れる電流は
$$I= \frac{1}{\sqrt{ {\color{blue} R} ^2+ ( {\color{purple} X_L} – {\color{green} X_C} )^2 }}V_0 \sin{(ωt+θ_I)}$$
$(\tan{θ_0}=-\frac{ X_L-X_C }{R})$
と求めることができました。

並列回路と同じように$ {\color{orange} Z_s} = \sqrt{ {\color{blue} R} ^2+ ( {\color{purple} X_L} – {\color{green} X_C} )^2 } $と置くと
$$I= \frac{1}{ {\color{orange} Z_s} }V_0 \sin{(ωt+θ_I)}$$
と表せます。 $Z_s$がインピーダンスとなり、交流回路の抵抗値に相当します。

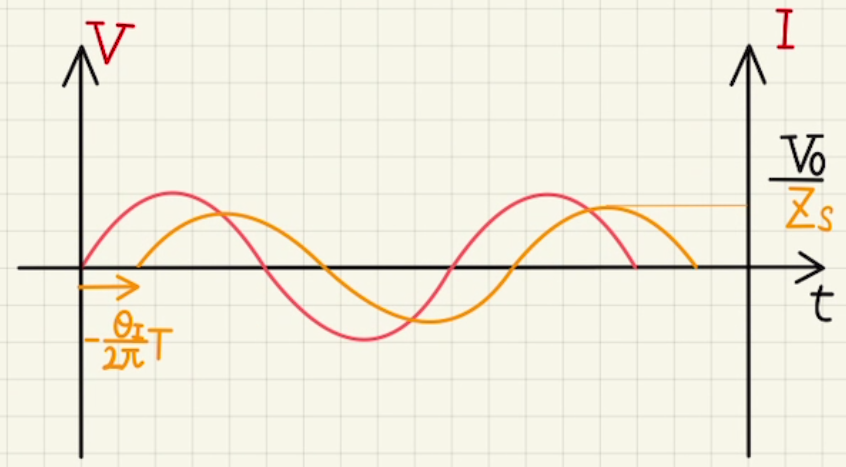
インピーダンス$Z_s$を用いると、それぞれのパーツでの電位差は、
$$ {\color{blue} V_R} =\frac{R}{Z_s}V_0\sin{(ωt+θ_I)} $$
$$ {\color{green} V_C} = – \frac{X_C}{Z_s}V_0 \cos{(ωt+θ_I)}$$
$$ {\color{purple} V_L} = \frac{C_L}{Z_s}V_0 \cos{(ωt+θ_I)} $$

・力率
コイルやコンデンサーを含む回路では、電力を消費するのは抵抗だけなので、1秒当たりの平均消費電力が$V_eI_e$と一致しません。
実際に消費される電力は三角関数の積の式$\sin{α}\sin{β}=\cos{(β-α)}-\cos{(β+α)}$を用いると計算できます。
\begin{align}
P&=IV_R=\frac{1}{ Z_s }V_0 \sin{(ωt+θ_I)}×\frac{R}{Z_s}V_0\sin{ωt} \\
&=\frac{V_0^2}{ Z_s } \sin{(ωt+θ_I)}\sin{ωt} \\
&= \frac{V_0^2}{ Z_s } \left( \cos{(θ_I)}-\cos{(2ωt+θ_I)} \right) \\
\end{align}
このことから1周期での消費電力は
\begin{align}
W=\int_0^T(Pdt)&=\frac{V_0^2}{ Z_s }\int_0^T \left( \cos{(θ_I)}-\cos{(2ωt+θ_I)} \right)dt \\
&= \frac{V_0^2}{ Z_s }\left[ \cos{(θ_I)}t-\frac{1}{2ω}\sin{(2ωt+θ_I)} \right]_0^T \\
&= \frac{V_0^2}{2R}\cos{(θ_I)}T = V_eI_e\cos{(θ_I)}T \\
\end{align}

よって1秒当たりの平均消費電力は
$$\bar{P}=V_eI_e\cos{(θ_I)}$$
となることから平均消費電力は抵抗だけの回路より$\cos{(θ_I)}$倍であることが
わかりました。
この
$$\cos{(θ_I)}=\frac{ R }{Z_s}$$
を力率といいます。
また、$S=V_eI_e$を皮相電力、$\bar{P}=V_eI_e\cos{(θ_I)}$を有効電力と言います。

・補足
抵抗とコンデンサーとコイルのどれかが抜けているパターンもあります。
同様に計算してもいいのですが、
抵抗がない回路は$R→0$
コンデンサーがない回路は$X_C→0$($C→∞$)
コイルがない回路は$X_L→0$($L→0$)
とすることで電流や電圧等は同じ結果になります。

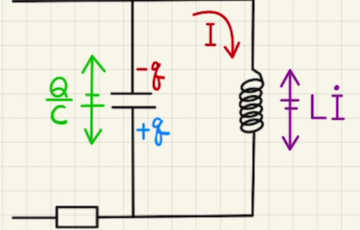
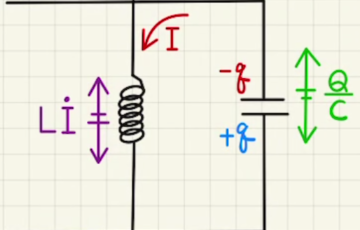
LC回路の電気振動

上図のようなコンデンサーとコイルが直列している回路を考えます。
$\frac{dI}{dt}$を$\dot{I} $と表記すると、この回路の方程式は
$$0=\frac{Q}{C}+L \dot{I} \tag{①} $$
より、
$\dot{I} =-\frac{1}{CL}Q$となるため、
ここで両辺を微分して、$\frac{dQ}{dt}=I$を当てはめると
$$ \ddot{I} =-\frac{1}{CL}I $$
この式は単振動と同じ二階微分方程式になります。

$ω= \frac{1}{\sqrt{CL}}$とおくと、微分方程式の解は
$$I(t) = C_1 \cos{ωt} + C_2\sin{ωt} \tag{②}$$
となります。$C_1, C_2$は積分定数となるので、これらを初期値から求めていきます。
最初に流れている電流は$t=0$を代入して
$I(0) = C_1 $
となります。
また、ここで②を微分して
$\dot{I}(t) = -C_1ω \sin{ωt} + C_2ω\cos{ωt} $
$t=0$を代入すると、
$\dot{I}(0) = C_2ω $
また、①の回路方程式から
$ \dot{I}(0) =-\frac{1}{CL}Q(0)$となるので、それを代入すると、
$ C_2 = \frac{1}{ω}\dot{I}(0)= -\frac{1}{CLω}Q(0) = -ωQ(0) $
となります。
これらの定数を代入して、最終的な電流の推移は
$$I(t) = I(0) \cos{ωt} – Q(0)ω \sin{ωt} $$
また、積分することでコンデンサーに貯められた電荷も求めることができます。
$$Q(t) = \frac{I(0)}{ω} \sin{ωt} + Q(0) \cos{ωt} $$

・補足
電流と電荷の関係を知りたいだけなら、
エネルギー保存の式
$$\frac{Q^2}{2C}+\frac{1}{2}LI^2=一定$$
も使うことができます。

まとめ

$V=V_0\sin{ωt}$のように時間変化する電圧を与える電源を交流電源といい、実質的な電圧に相当する実効値は $V_e = \frac {V_0}{\sqrt{2}}$となる。

$V=V_0\sin{ωt}$の交流を流すとコンデンサーでは、$X_C=\frac{1}{ ω C }$の抵抗値に相当するリアクタンスが生まれ、電流の位相は$\frac{π}{2}$だけ進んだ波形になる。
同様にコイルでは、 $ X_L=Lω$の抵抗値に相当するリアクタンスが生まれ、電流の位相は$\frac{π}{2}$だけ遅れた波形になる。

抵抗とコンデンサーとコイルの三つを並列に並べた回路では
$$Z_p=\frac{1}{ \sqrt{ \Bigl( \frac{1}{R} \Bigr) ^2 + \Bigl( \frac{1}{ X_C} – \frac{1}{ X_L} \Bigr) ^2} }$$
に相当する抵抗値がうまれ、これをインピーダンスと言う。

同様に、抵抗とコンデンサーとコイルの三つを直列に並べた回路では
$$Z_s= \sqrt{R^2+ (X_L-X_C)^2 } $$
インピーダンスがうまれる。

交流電源のないコンデンサーとコイルの回路では電流は振動し、$ω= \frac{1}{\sqrt{CL}}$とすると
$$I(t) = I(0) \cos{ωt} – Q(0)ω \sin{ωt} $$
となり、コンデンサーにたくわえられた電荷は
$$Q(t) = \frac{I(0)}{ω} \sin{ωt} + Q(0) \cos{ωt} $$
となります。