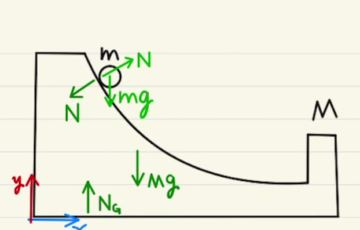
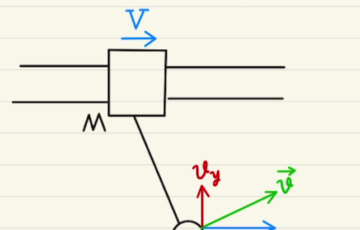
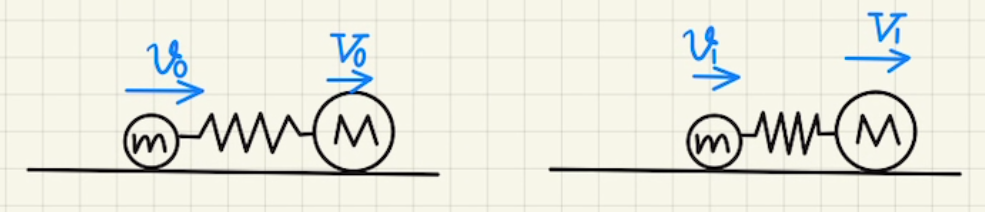二物体の運動と力学的エネルギー保存について考えていきます。
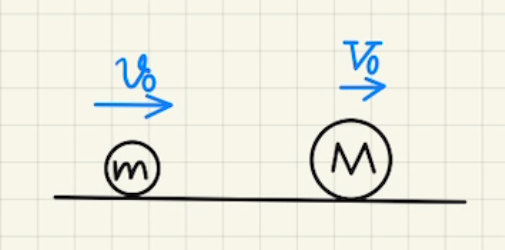
二物体の力学的エネルギー
二物体のエネルギーの足し合わせると
$$E_0=\frac{1}{2}mv_0^2+ \frac{1}{2}mV_0^2 $$
これを重心エネルギーと、相対エネルギーの形にしていきたいと思います。
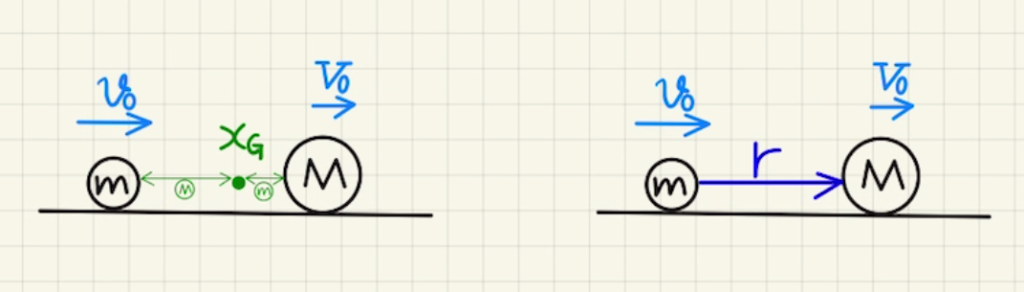
合計の質量:$m_G = m + M$
重心速度:$v_G=\frac{mv_0+MV_0}{m+M}$
換算質量:$\frac{1}{m_r} = \frac{1}{m} + \frac{1}{M}$
相対速度:$v_r = V_0-v_0$
のように置くと、以下のように式を書き換えることができます。
$$E_0= \frac{1}{2}m_Gv_G^2 + \frac{1}{2}m_rv_r^2$$
重心速度は重心位置$x_G$の時間微分したものとなります。
相対速度は、二物体の相対位置の時間微分となります。
運動量保存時のエネルギー損失
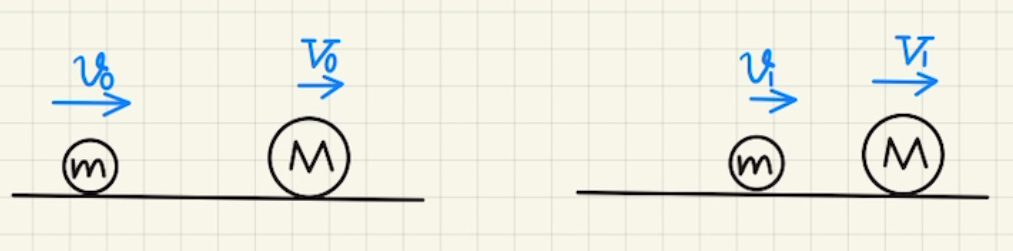
二物体が衝突したときを考えてみましょう。
運動量が保存するため、 重心速度は
$$v_G=\frac{mv_0+MV_0}{m+M} = \frac{mv_1+MV_1}{m+M} $$
で一定となります。
そのため、 重心エネルギーは保たれる形になります。
一方で、 相対運動は$v_r = V_0-v_0$から、 $v_r’ = -e(V_1-v_0)$となることから
相対エネルギーの損失は
\begin{align}
ΔE_r &=& \frac{1}{2}m_rv_r^2 – \frac{1}{2}m_rv_r’^2 \\
&=& \frac{1}{2}(1-e^2)m_rv_r^2 \\
\end{align}
全体の損失はこの 相対エネルギーの損失の損失と一致します。
よって衝突によって失われたエネルギーは
$$ ΔE = \frac{1}{2}(1-e^2)m_rv_r^2 $$
となります。
これは衝突時だけではなく、運動量が保存するとき全てに応用できます。
例えば、バネにつながれた二物体が相対速度$ v_r $だったのときバネの伸びが$0$だったのが、相対速度$ 0$になったときバネの伸び$r$となったとすれば
$$ \frac{1}{2}kr^2 = \frac{1}{2}m_r(v_r^2 – 0^2) $$
などと計算できます。