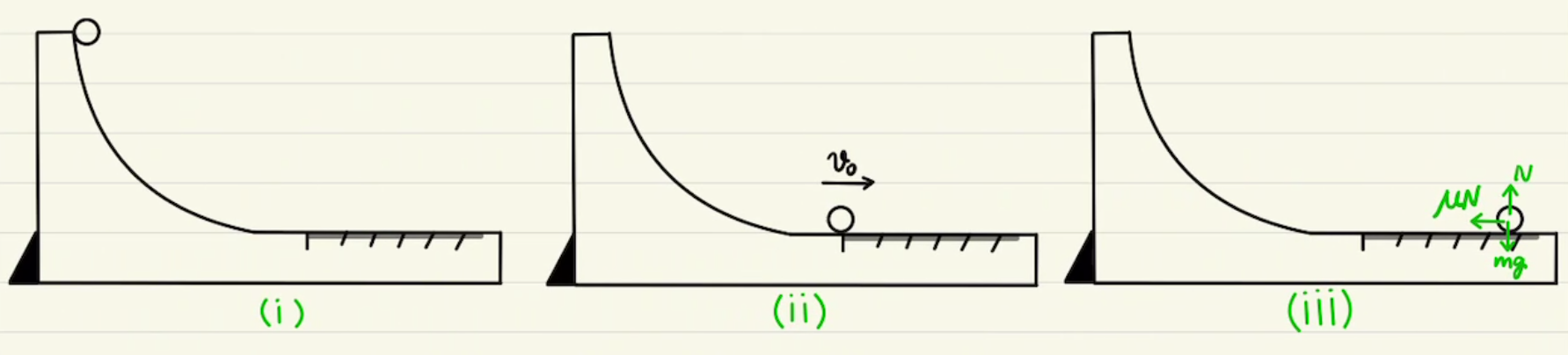
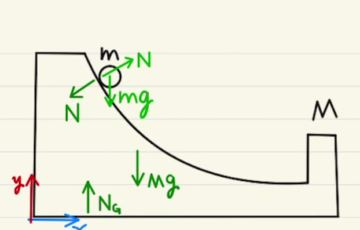
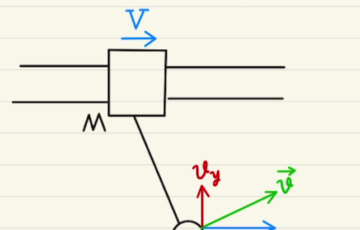
今回から力学的エネルギー保存の話となります。
力学的エネルギーと似ている所も多いので注意してみていきましょう。
これも力学的エネルギーと同じく、運動方程式
$$ ma = f $$
から導かれたものです。
導出から書いていきますが、軽く流し読みで結構です。
今回は、運動方程式をそのまま時間微分していきます。
両辺をある時刻$0$から時刻$t_1$まで時間積分すると
$$ \left[{mv}\right]_{0}^{t_1} = \int_0^{t_1}{f}dt $$
この式が運動量保存の式となります。
左辺は変化量なので、見やすさのために下の式のように書くこともあります。
$$ Δ\left[{mv}\right] = \int_0^{t_1}{f}dt $$
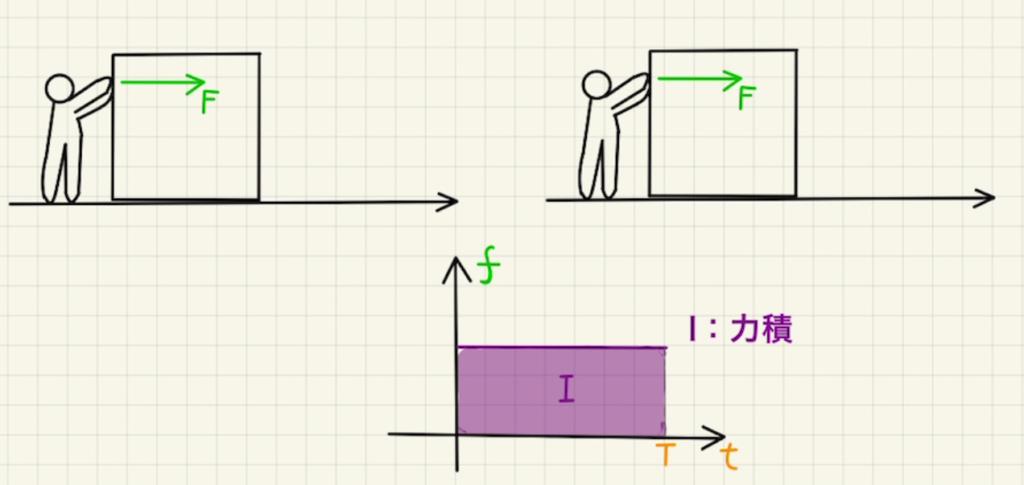
$mv $が物体の持つ運動量、$ \int{f}dt $が力が物体に与える運動量となり、これを力積とよびます。
つまり力積を与えた分だけ運動量が増えるということになりますね。
運動エネルギー保存の式と比較しながら見ていきます。
平面、もしくは立体で考える場合、速度と力はベクトルとなるので、それぞれの式を表すと
$$力学的エネルギー保存: Δ\left[{\frac{1}{2}m \vec{v}^2}\right] = \int_0^h{ \vec {f}}d \vec {x} $$
$$運動量保存: Δ\left[{m \vec{v}}\right] = \int_0^{t_1}{ \vec{f}}dt $$
運動量保存はベクトルの式
ベクトルでない大きさだけの量を”スカラー”といいます。
力学的エネルギー保存の式は「スカラー=スカラー」の式となっています。
実際に左辺はベクトルの二乗、左辺はベクトルの内積になっているのがわかるとおもいます。
一方で運動量保存の式は「ベクトル=ベクトル」の式となります。
よって$x$方向、$y$方向、(場合によっては$z$方向)に分解して運動量保存の式が書けます。
また、$x$方向だけ運動量が保存するといったこともしばしばあります。
$$ \vec{v} = \begin{bmatrix} v_x \\v_y \end{bmatrix} ,\vec{f} = \begin{bmatrix} f_x \\f_y \end{bmatrix}$$
と置いて要素ごとに書き直すと
$$ Δ\left[{mv_x}\right] = \int_0^{t_1}{ f_x}dt $$
$$ Δ\left[{mv_y}\right] = \int_0^{t_1}{ f_y}dt $$
物体が動かなくても力積を与える
力学的エネルギー保存の式と運動量保存の右辺を比べてもらうと積分する変数が違うことがわかります。
力学的エネルギー保存では位置で積分しているため、動かすことができなければ、エネルギーを与える(仕事をする)ことはありませんでした。
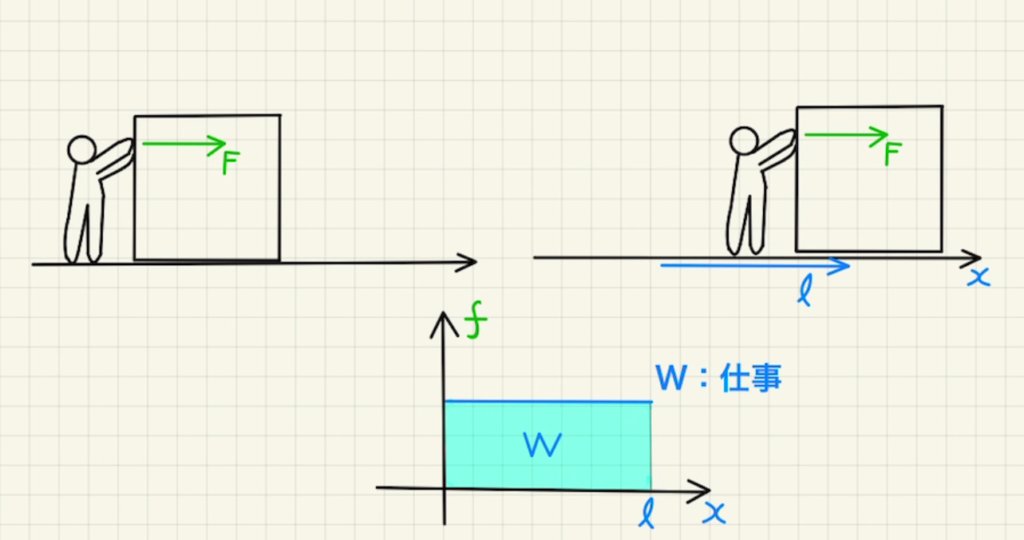
一方で、 運動量保存の式では時間で積分しているため、全く動かすことはなくても力を与え続けた時間分だけ運動量を与える(力積を及ぼす)ことになります。
これは二つの保存則の大きな違いとなっています。
複数の物体の運動量保存で使われることがほとんど
複数の物体を一つの物体のようにまとめて扱うことがあります。これを”系”とよびます。
二物体の系に対して外から力が働かない場合、 二物体同士で作用反作用しか働きません。
片方への力の作用を $\vec{f}$とすると、反作用は$-\vec{f}$となります。
それらの運動量保存式を見てみると
$$ Δ\left[{m_1 \vec{v_1}}\right] = \int_0^{t_1}{ \vec{f}}dt $$
$$ Δ\left[{m_2 \vec{v_2}}\right] = \int_0^{t_1}{ -\vec{f}}dt $$
となります。
二つの式を足すと
$$ Δ\left[{ m_1 \vec{v_1} + m_2 \vec{v_2} }\right] = 0 $$
このことから$m \vec{ v }$の合計は変化しないことがわかりました。
及ぼしあう力積が同じ大きさで向きが反対だからですね。
それをより一般化して書くと下のような式になります。
$$ \sum{m \vec{v}} = 一定 $$
しかし、ある時間での二物体の速度を求める場合、求める値は二つにあります。
この一式だけでは求まらないことが多く、他の式と連立するのが一般的です。
運動量が保存するケースは限られている
動かさなくても力積を与えますし、力を少しの時間でもかけたら力積を与えます。
なので物体に対して系の外から一切の力を及ぼさない状況に限り、運動量保存は成り立ちます。
そのような状況はほとんどない(重力も地面からの垂直抗力もない状況)ので、運動量保存が成り立つ状況は限られます。(厳密には地球も系の一部にしてしまえば成り立ちますが、そのように設定することはあまりないです。)
よく運動量保存に使われるケースは二種類に分けられます。
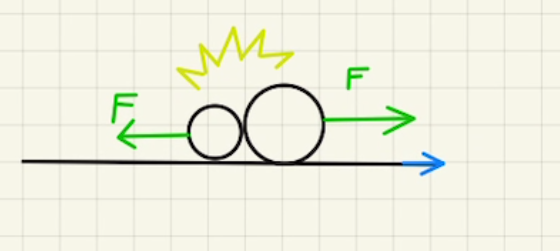
・短時間に力積を及ぼす。
つまり衝突です。
外からは力積を与える時間がないほど短時間に、二物体が力積を及ぼすので衝突による力積のやりとりだけ考慮すればよくなります。(この場合、理論的に衝突でかかる力は無限大となりますね。)
その後の動きは反発係数$e$によって決まるので、 運動量保存の式と反発係数の式を連立します。
・1方向だけに注目すると、外部から力が働かない。
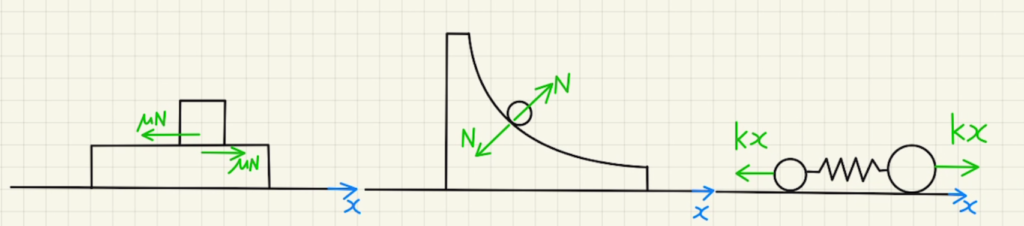
水平方向には力が外部から働かず、 二物体の間で垂直抗力や摩擦力等による作用反作用が働き、他からは水平方向の力を受けない状況です。
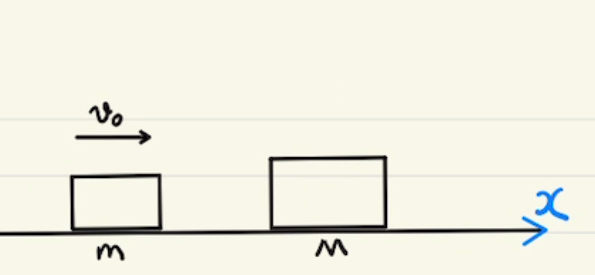
例えば地面と摩擦がない台の上に物体がのっている場合です。
二物体の間で垂直抗力や摩擦が働いていたとしても二物体の運動量の合計は変わりません。ただし$x$方向のみとなります。
力学的エネルギー保存の式と連立することが多いです。
他にも物体の貫通などでも運動量は保存します。
まとめ
ある一方向に対して、 系の運動量$\sum{m \vec{ v}}$が条件を満たすと一定になります。
その条件とは系の外部から力を受けないことです。
運動量が保存する主な例は以下。
・衝突
・地面との間で摩擦のない動く台の上で物体が動く(水平方向のみ)
・固定されてない物体を貫通する。(水平方向のみ)